دانلود ترجمه مقاله مدل شبیه سازی GSFLOW - مدل سازی تلفیقی آب های سطحی و زیرزمینی
عنوان انگلیسی مقاله:
GSFLOW—a basin-scale model for coupled simulation of ground-water and surface-water flow—part b. concepts for modeling saturated and unsaturated subsurface flow with the u.s. geological survey modular ground-water model
عنوان ترجمه شده مقاله:
مدل GSFLOW: یک مدل در مقیاس حوضه برای شبیه سازی توأمان آب های زیر زمینی و جریان آب های سطحی. بخش دوم: مفاهیم مدل سازی جریان زیرسطحی اشباع شده و غیر اشباع با ماژول مدل آب های زیرزمینی USGS
چکیده:
MODFLOW یک مدل جریان آب های زیر زمینی است که می تواند برای ارزیابی مسائل منابع آب های زیر زمینی و جهت اتخاذ تصمیمات مدیریتی در توسعه منابع آب های زیر زمینی در انواع مقیاس ها مورد استفاده قرار بگیرد. این مدل همچنین دارای توانایی بررسی اثر برداشت آب های زیر زمینی در آب های سطحی با استفاده از گزینه های مختلفی که به شبیه سازی فعل و انفعالات آب زیرزمینی با جریان ها و دریاچه ها می پردازد است. فرآیندهای محاسباتی و پروسه های سطحی در MODFLOW بودجه های آب های سطحی و انرژی برای قسمت بندی بارش به تبخیر و تعرق، رواناب، جریان های زیرسطحی، و جریان های غیر اشباع در زیر زون خاک را شامل نمی شود. به طور معمول، رواناب، نفوذ، و جریان غیر اشباع حاصل از سطوح آب زیرزمینی (با فرض تغذیه آب های زیر زمینی) در خارج از حیطه برآورد MODFLOW می باشد. MODFLOW به سیستم مدل بارش-رواناب (PRMS) که توسط سازمان زمین شناسی ایالات متحده (USGS) ارائه شده است؛ به منظور بهبود برآورد نحوه تغذیه در مطالعات مدل سازی آب های زیر زمینی و جهت ارائه محاسبات کاملی از بودجه های آبی در یک منطقه و یا حوضه متصل گردیده است. این مدل جفت شده به نام GSFLOW شناخته می شود. همچنین کدهای اضافی نیز برای تسهیل اتصال دو مدل به GSFLOW اضافه شده است. ارتباط در MODFLOW از طریق یک پکیج جدید غیر اشباع از منطقه جریان (UZF1) می باشد؛ که برای مسیریابی جریان از زون خاک بکار رفته در PRMS به سمت سطح آب زیرزمینی طراحی شده است.
مقدمه:
نیاز اتصال MODFLOW به یک مدل بارش-رواناب، در نتیجه افزایش نگرانی در مورد اثرات کاربری زمین و تغییرات آب و هوایی در توزیع تغذیه آب های زیر زمینی صورت گرفته است. از آنجا که شرایط جریان و ذخیره سازی آب در هر دوی بخش های بالایی و پایینی سطح زمین، تغذیه را تحت تاثیر قرار می دهد؛ در این شرایط اغلب لازم است تا شرایط به همراه یکدیگر (جفت شده) برای پیش بینی تغییرات در منابع آب شبیه سازی شوند. در حال حاضر، چند کد معدود برای مدل سازی در مقیاس های بزرگ تعاملی آب سطحی / آب زیرزمینی با قابلیت شبیه سازی زمان و فضای متغیر بارش، تبخیر و تعرق، جریان های زمینی و جریان زیرسطحی، ذخیره سازی زون خاک، و جریان غیر اشباع در قسمت زیرین زون خاک، در دسترس است. به همین دلیل، مدل مدولار آب های زیرزمینی (MODFLOW، McDonald و Harbaugh، 1988؛ و Harbaugh و همکاران، 2000) به سیستم مدل سازی بارش-رواناب (PRMS) برای شبیه سازی، جفت شده است (Leavesley و همکاران، 1983). این مدل جفت شده و یا اتصالی با نام GSFLOW شناخته می شود. GSFLOW به منظور حفاظت جمعی در سراسر دامنه مدل طراحی گردیده است. بودجه کلی آب همراه با سهمیه آب اختیاری برای هر یک از اجزای اصلی منتشر شده است.
ماژول جدیدی برای PRMS و یک بسته جدید نیز برای MODFLOW به منظور تسهیل اتصال بین PRMS و MODFLOW برای GSFLOW توسعه داده شده است. ماژول اولیه زون خاک در PRMS برای ایجاد امکان اتصال به یک بسته جدید در MODFLOW به نام بسته منطقه غیر اشباع جریان (UZF1) بازنویسی گردیده. اصلاح ماژول زون خاک در PRMS در یک مقاله (Markstrom و همکاران، 2006) همراه با استفاده از داده های مکانی GIS در توسعه مجموعه داده های لازم برای GSFLOW مورد بحث قرار گرفته است. زون خاک یک منطقه نسبتا کم عمق است که به طور معمول شامل عمق ریشه گیاهان می باشد. آب ذخیره شده در زون خاک در PRMS به تبخیر و تعرق، جریان زیرسطحی، و جریان به سمت پایین در زیر زون خاک تقسیم می گردد. که جریان به سمت پایین تر از زون خاک به سوی منطقه عمیق تر غیر اشباع (UZF1) وابسته به ذخیره سازی در زون خاک و هدایت هیدرولیکی عمودی منطقه عمیق تر غیر اشباع است.
این مقاله به بررسی توسعه (UZF1 Niswonger و همکاران، در دست چاپ)، که جریان غیر اشباع و ذخیره سازی در زیر زون خاک و جریان وابسته به هد زون خاک هنگامی که سطح آب زیرزمینی، بالا و یا پایین زون خاک باشد را شبیه سازی می کند، می پردازد. علاوه بر این، انطباق با پکیج مسیریاب آبراهه ای MODFLOW جهت (SFR1، Prudic و همکاران، 2004.) شبیه سازی جریان توزیع شده در کانال ها و جریان های غیر اشباع در زیر کانال ها تشریح شده است.
مفاهیم جریان آب های زیر زمینی در با رابطه با استفاده از GSFLOW در یک حوضه به مساحت 27 کیلومتر مربع در Sierra Nevada مورد بحث قرار گرفته است.
___________________________________
جریان غیر اشباع در زیر زون خاک
روش:
روش های متعددی برای شبیه سازی جریان غیر اشباع جهت پیش بینی تغذیه در مدل جریان آب های زیر زمینی استفاده شده است. روش پر کاربرد، حل معادله ریچاردز با استفاده از روش تفاضل محدود و یا عناصر محدود جهت شبیه سازی سه بعدی (D-3) جریان متغیر اشباع می باشد (Panday و Huyakorn، 2000؛ Thoms و همکاران، در دست چاپ). معادله ریچاردز برای شبیه سازی جریان غیر اشباع و تبخیر و تعرق بسیار دقیق است. با این حال، این معادله کاملا غیر خطی بوده و همین امر ممکن است باعث ناکارآمدی معادله ریچاردز در مسائل بزرگ شود.
روش ساده تر برای مدل سازی جریان غیر اشباع، بکارگیری یک فرم یک بعدی (D-1) معادله ریچاردز است که توسط تکنیک تفاضل محدود حل شده است (Pikul و همکاران، 1974. Refsgaard و Storm در 1995). معادله یک بعدی ریچاردز برای شبیه سازی جریان عمودی از طریق منطقه غیر اشباع، و جریان در سراسر سطوح آب زیرزمینی از منطقه غیر اشباع به عنوان تغذیه، بکار رفته در معادله جریان آب های زیر زمینی D-3 استفاده می شود. این رویکرد به طور قابل توجهی تعداد محاسبات مورد نیاز برای شبیه سازی جریان غیر اشباع در مسائل بزرگ را کاهش می دهد. با این حال، این اتصال چندان سر راست نیز نمی باشد، زیرا معادله ریچاردز نیازمند یک طول کوتاه تری از زمان و مکان در قیاس با آنچه در طی محاسبه یک راه حل برای جریان آب های زیرزمینی به کار می رود، است. علاوه بر این، تناقضاتی نیز در میان دو معادله جهت پیش بینی ارتفاع سطوح آب زیرزمینی بوجود می آیند.
جریان غیر اشباع در GSFLOW به صورت جریان عمودی شبیه به مدل های Pikul و همکاران. (1974) و (Refsgaard و Storm در 1995) شبیه سازی شده. با این حال، معادله ریچاردز برای همانند سازی یک معادله سینماتیک موجی با نادیده گرفتن مدت پخش، ساده سازی شده است (Colbeck، 1972؛ Smith، 1983). این امر امکان حل معادله ریچاردز را با استفاده از روش مشخصه ها می دهد. از آنجا که راه حل روش مشخصه ها برای معادله ریچاردزِ سازی شده نیازمند تفکیک عمودی از منطقه غیر اشباع نیست؛ از مشکلات مذکور در ارتباط با معادله ریچاردز جفت شده، در معادله جریان آب های زیر زمینی اجتناب گشته است. این رویکرد برای شبیه سازی جریان غیر اشباع در UZF1 اجرا شد.
UZF1 شبیه سازی 1-D جریان عمودی غیر اشباع، تبخیر و تعرق، و تخلیه آب های زیر زمینی به زون خاک در MODFLOW است. بنابراین، از تمام جریان های آب بین MODFLOW و ماژول زون خاک در PRMS استفاده می کند. تقریب سینماتیک از معادله ریچاردز را می توان با در نظر گرفتن تلفات تبخیر و تعرق به صورت ذیل نوشت (Colbeck، 1972؛ Smith، 1983؛ Charbeneau، 1984):
[1]
∂θ/∂t+(∂K(θ))/∂z+i=0
که در آن θ محتوای حجم مرطوب (حجم آب به ازای هر حجمی از سنگ)، Z ارتفاع در جهت عمودی (طول)، (K(θ هدایت هیدرولیکی غیر اشباع به عنوان یک تابع از مقدار رطوبت (طول به ازای زمان)، i نرخ تغییر ET به ازای هر واحد عمق (طول به ازای زمان به ازای طول)، و t نیز بیانگر زمان می باشد. کاربرد روش مشخصه ها برای معادله 1 در مجموعه ی زیر از معادلات دیفرانسیل معمولی جفت شده نتیجه می شود (Niswonger و همکاران، در دست چاپ):
[2a]
dz/dt=∂K(θ)/∂θ=v(θ)
[2b]
dθ/dt=-i
[2C]
dθ/dz=(-i)/(v(θ))
که در آن (v(θ سرعت کاراکتری محدود شده به سمت پایین (z مثبت) مسیر است (طول به ازای زمان). معادله 2a سرعت امواج که نشان دهنده تری و خشکی در منطقه غیر اشباع است را ارائه می دهد. معادله b2 تغییرات در حجم آب را در مقابل موج در طول زمان نشان می دهد، و معادله c2 تغییرات در حجم آب در امتداد یک پروفیل موج (در پشت جبهه) را ارائه می دهد. معادلات 2a، b2 و c2 از یکدیگر جدا می باشند، که می توان آنها را برای پیدا کردن عبارات تحلیلی که توسط UZF1 استفاده می شود جهت شبیه سازی جریان غیر اشباع در حالت عمودی ادغام کرد.
اتصال UZF1 به MODFLOW:
تغذیه سطوح آب زیرزمینی در یک آبخوان آزاد از سمت راست سیستم معادلاتی که توسط MODFLOW حل شده است کسر می شود:
[3]
AX=B-Q_UZF1
که در آن A یک ماتریس محتوی ضرائب معادلات انتقال (آرایه HCOF) می باشد که توسط MODFLOW حل شده است. X بردار یک بعدی حاوی هد های آب زیرزمینی است که توسط MODFLOW حل شده است. B بردار یک بعدی شامل تمام شرایط معلوم در معادلات انتقال است که در مقادیر نامعلوم هد (آرایه RHS) ضرب نمی شوند. و QUZF1 نرخ حجمی (حجم در زمان) تغذیه محاسبه شده در یک سلول مدل داده شده از UZF1 است.
بنابراین، UZF1 در داخل حلقه تکرار غیر خطی MODFLOW جفت شده است. با این حال، به این دلیل که تغذیه آب های زیر زمینی وابسته به مقدار ذخیره سازی و میزان شدت نفوذ رو به پایین در منطقه غیر اشباع است، هیچ معادله کلی که رابطه ی بین تغذیه و هد آب زیرزمینی را مانند معادله انتقال در پکیج آبراهه (SFR1) تعریف می کند، وجود ندارد (Prudic و همکاران، 2004). بنابراین، UZF1 بر آرایه HCOF تأثیر نمی گذارد.
پکیج UZF1 همچنین امکان نشت آب های زیر زمینی به زون خاک، هر زمان که سطح آب در یک سلول بالاتر از ارتفاع کف زون خاک است را می دهد. نرخ حجمی نشت آب های زیر زمینی به زون خاک بر اساس معادله زیر محاسبه می شود:
[4]
Q_gw=(A_cell K_v (h-celtop))/((0/5celthk))
که در آن h ارتفاع سطوح آب؛ celtop ارتفاع انتهای زون خاک؛ Acell ناحیه نقشه سلول های مدل (معادل با طول ستون زمان، طول سطر شبکه مدل)؛ KV هدایت هیدرولیکی عمودی سلول های مدل؛ و celthk ضخامت سلول مدل است. مقداری که از آرایه HCOF در MODFLOW کسر شده (مربوط به ماتریس A در معادله 3) معادل است با:
(A_cell K_v (h-celtop))/((0/5celthk))
___________________________________
جریان آبراهه ای
مسیریابی جریان آبراهه ای در کانال:
مشابه با روش مورد استفاده برای شبیه سازی جریان غیر اشباع، از یک تقریب موج سینماتیک معادلات سنت ونانت برای شبیه سازی جریان آبراهه ای استفاده شد است (Lighthill و Whitham در 1955). با این حال، بر خلاف UZF1، پکیج نسخه انطباقی مسیریابی جریان آبراهه ای، که SFR2 نامیده می شود (Niswonger و Prudic در 2006)، معادله سینماتیک موج را با استفاده از روش تفاضل محدود ضمنی حل می کند. معادله سینماتیک موج برای مسیریابی جریان در آبراهه می تواند به صورت زیر نوشته شود:
[5]
∂Q/∂x+∂A/∂t=q
که در آن Q دبی (مکعب طول در زمان)؛ A سطح مقطع جریان (مربع طول)؛ q جریان ورودی جانبی در واحد طول (طول مربع در زمان)؛ و X (طول) و T (زمان) مختصات مکان و زمان است. SFR2 مومنتوم مرتبط با شیب بستر و اصطکاک کانال را بر اساس معادله مانینگ، منحنی های مشخص رتبه بندی، و یا روابط عمومی قانون قدرت که توسط Leopold و همکاران (1992) توضیح داده شده، می داند. مومنتوم با توجه به شیب سطح آب و شرایط شتاب در معادلات سنت ونانت، در تقریب سینماتیک موج نادیده گرفته شده است. SFR2 قادر است تا جریان را در کانال های غیر منشوری مسیریابی نماید.
اتصال SFR2 به MODFLOW:
بازه جریانات جفت شده به سلول های MODFLOW بر اساس یک معادله Darcy-type برای جریان از طریق یک رودخانه است، که می تواند به صورت زیر نوشته شود:
[6]
Q_L=KwL/m(h_s-h_a)
که در آن QL جریان حجمی بین بخش معینی از آبراهه و حجم آبخوان (حجم به ازای زمان)؛ K هدایت هیدرولیکی رسوبات رودخانه (طول به ازای زمان)؛ W عرض آبراهه (طول)؛ L طول آبراهه مربوط به حجمی از آبخوان (طول)؛ m ضخامت رسوبات گسترش یافته از بالا به پایین بستر رودخانه (طول)؛ hs هد در آبراهه تعیین شده توسط افزودن عمق جریان به ارتفاع بستر رودخانه (طول)؛ و ha هد در آبخوان در زیر بستر رودخانه (طول) است.
همین روش برای شبیه سازی جریان غیر اشباع در UZF1 جهت شبیه سازی جریان عمودی در زیر کانال، هر زمان که هد در آبخوان درست در زیر بستر رودخانه است، استفاده می شود (Niswonger و Prudic در 2006).
Nonlinearities مرتبط با رابطه میان عمق آبراهه، عرض، هد سفره، و جریان بین آبراهه و آبخوان در داخل حلقه تکرار غیر خطی MODFLOW حل شده است.
Sagehen Creek Application:
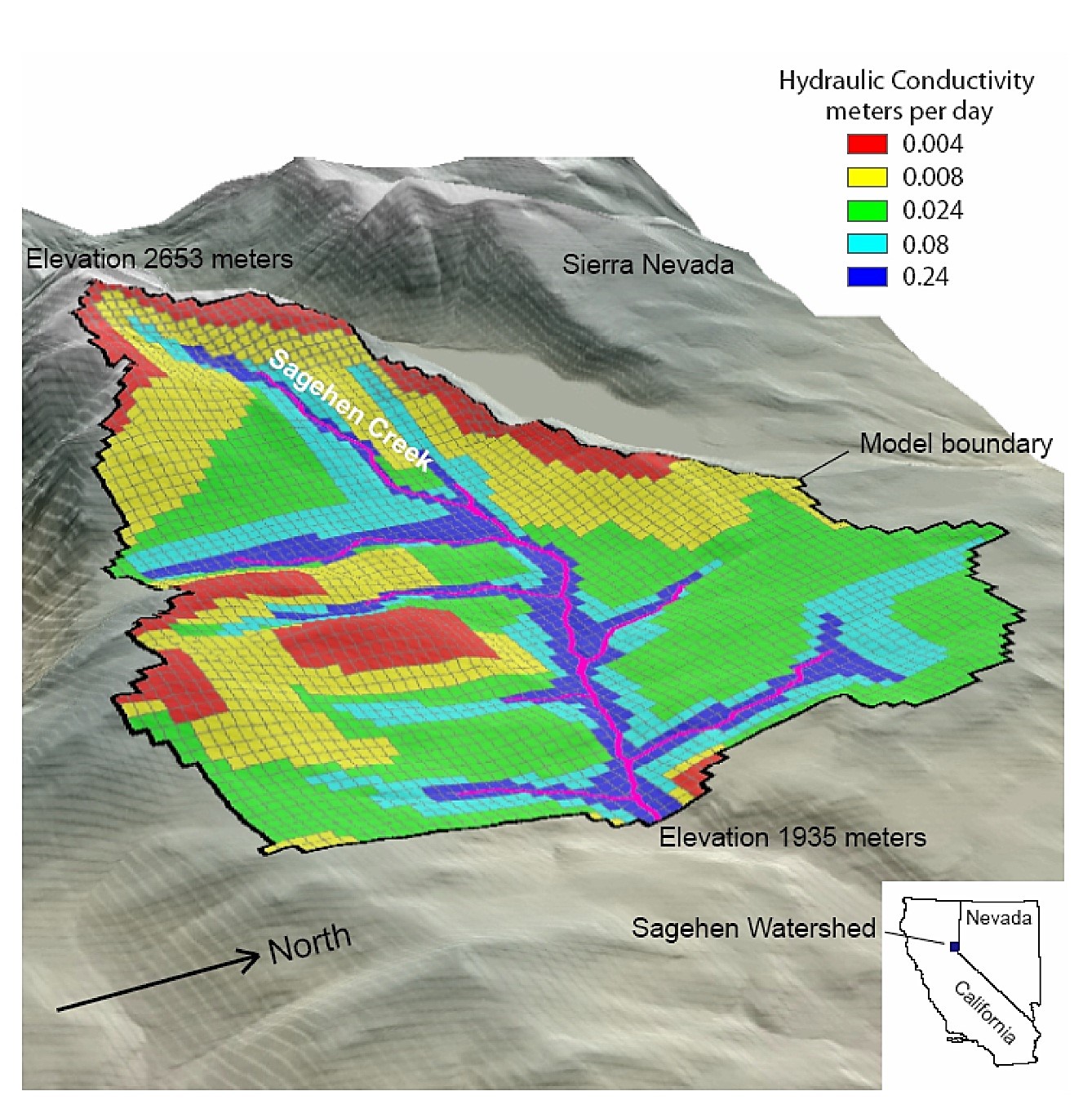
GSFLOW برای مدل سازی جریان سطحی و زیر سطحی در حوضه Sagehen، که یک شبکه حوضه هیدرولوژیک آزمایشی USGS واقع در شرق شیب شمالی Sierra Nevada در نزدیکی Truckee, California می باشد مورد استفاده قرار گرفته است (شکل 4). این حوضه، یک منطقه به مساحت 27 کیلومتر مربع و در محدوده ارتفاع 1926 تا 2663 متر بالاتر از سطح دریا را زهکشی می کند. حوضه Sagehen شامل سنگ های گرانیتی است که توسط سنگ های آتشفشانی و با یک روکش نازک از مواد آبرفتی گرفته شده است. بارش سالانه جوی به طور متوسط حدود 970 میلی متر است و بخش عمده ای از هیدروگراف سالانه متأثر از ذوب برف می باشد. ضمن آنکه سوابق روزانه آبدهی از آغاز اکتبر 1953 در دسترس می باشد.
شبیه سازی شامل یک لایه مدل تک با 73 سطر و 81 ستون بود که در آن تمام سلول های عرض ثابت و طول معادل 90 متر بود. ارتفاعات بالای سلول های مدل با ارتفاعات تخمینی زون خاک پایینی و ارتفاعات پایین سلول های مدل با استفاده از ارتفاعاتی که از حدود 100 متر پایین تر از زون خاک در دره تا آنجا که 200 متر زیر زون خاک در پشته ها قرار گرفتند، تنظیم شد. ارتفاعات زیرین در مدل دامنه ای از 1830 تا 2480 متر بالاتر از سطح دریا را شامل می شود. نتایج ارائه شده در این مقاله به دنبال یک دوره شبیه سازی طولانی آغاز شده از 7 مارس سال 1983 و پایان یافته در تاریخ 7 مارس 1984 می باشد. دوره شبیه سازی به 365 دوره تنش one-day-long تقسیم شد. هد اولیه و حجم آب منطقه غیر اشباع از نتایج حاصل از حالت شبیه سازی MODFLOW گرفته شد. یک گام زمانی برای هر دوره تنش شبیه سازی گردید. امکان هیچ جریانی در پایین و دو طرف مدل داده نشد به جز سه سلول در زیر و در مجاورت جریان در خروجی حوضه که به عنوان سلول های ثابت هد مشخص شدند.
واسنجی مدل:
پکیج لایه ویژگی های جریان (LPF) در MODFLOW مورد (Harbaugh و همکاران، 2000) استفاده قرار گرفت و مقادیر هدایت هیدرولیکی (K) در هر دو جهت افقی و عمودی مشخص گردید. از آنجا که تنها یک لایه در مدل مشخص شد، K عمودی در آبخوان تنها نشت آب های زیر زمینی به زون خاک و جریان در زون غیر اشباع را تحت تأثیر قرار داد. همه سلول ها به شکل قابل تبدیل (محصور نشده) مشخص شدند. مقدار افقی K از 004/0 متر در روز در پشته ها تا 24/0 متر در روز در دره ها برای شبیه سازی اولیه متغیر بود (شکل 1). K کمتر در پشته ها مشخص گردید چرا که در این مناطق سنگ های آتشفشانی مجاور سطح زمین قرار دارند، در حالی که سنگ های آتشفشانی در دره با مواد آبرفتی پوشیده شده است. K در داخل هر سلول همگن در نظر گرفته شد. ضریب ذخیره ویژه 0000005/0 بر متر در نظر گرفته شد، و راندمان ویژه 05/0 در پشته ها و 25/0 در دره در نزدیکی جریان مشخص گردید.
توسعه مدل GSFLOW برای حوضه Sagehen نیازمند کالیبراسیون مدل PRMS و مدل MODFLOW می باشد. فرآیند کالیبراسیون توسط اولین مدل کالیبره به طور مستقل صورت گرفت؛ PRMS برای یک دوره ده ساله کالیبره شد و MODFLOW برای حالت ماندگار کالیبره گردید. مقاله ای در همین موضوع (Markstrom و همکاران، 2006) به طور خلاصه روش کالیبراسیون مورد استفاده برای اندازه گیری و واسنجی PRMS را تشریح کرده است. فقط طریقه کالیبراسیون مدل MODFLOW در مقاله حاضر شرح داده شده است.

شکل 1. مدل سازی منطقه مورد مطالعه در حوضه Sagehen، تفکیک مکانی و پراکنش هدایت هیدرولیکی (K).
پراکنش K برای UZF1 و MODFLOW در ابتدا بر اساس زمین شناسی سطوح ایجاد شده بود و در طول کالیبراسیون تنظیم گردید. شبیه سازی حالت ماندگار بر اساس این فرض که متغیر مکانی تغذیه آب های زیرزمینی متناسب با توزیع میانگین بارش سالانه بوده، می باشد. میزان بارش با توجه به 860 میلی متر بارندگی در ارتفاع کمتر از 2100 متر و 1140 میلی متر بارش بالاتر از ارتفاع 2100 متر توزیع شد. دامنه تغذیه آب های زیرزمینی برای شبیه سازی حالت ماندگار توسط مقدار تقریبی میانگین تخلیه روزانه در خروجی حوضه Sagehen در اوایل ماه دسامبر تعیین گردید. پالایش کالیبراسیون مدل مستقل در طول شبیه سازی GSFLOW با متغیرهایی که تبادل آب بین PRMS و MODFLOW را کنترل می نماید، ایجاد شد. این متغیرها ضرائبی در معادلات نرخ می باشند که جریان بین زون خاک و دیگر زون های غیر اشباع یا بین زون خاک و آب زیرزمینی هنگامی که سطح آب بالاتر از ارتفاع کف زون خاک است، را کنترل می کنند.
شبیه سازی حالت ماندگار منجر به حصول سطوح آب محاسبه شده است؛ که به اندازه 80 متر زیر سطح زمین در امتداد پشته ها و درست برابر و یا کمی بالاتر از سطح زمین در پایین ترین بخش هایی از دره کنار رودخانه ها بود. اگر چه هیچ چاه مشاهده ای در پشته های حوضه حفر نشده است، اما حداکثر عمق تا آب زیرزمینی در چاهی در نزدیکی پشته ها در جایی دیگر در شمال Sierra Nevada اندازه گیری شد.
تحلیل حساسیت هدایت هیدرولیکی عمودی و افقی:
فقط این نتایج مرتبط با جریان زیرسطحی در زیر زون خاک ها در اینجا معرفی شده اند. مقاله همراهی در همین موضوع (Markstrom و همکاران، 2006) شامل مقایسه بین جریان آبراهه ای اندازه گیری شده و شبیه سازی شده است. تجزیه و تحلیل حساسیت برای تجزیه و تحلیل اثرات متغیر هدایت هیدرولیکی افقی و عمودی در زیر زون خاک بر نفوذ، تغذیه، و تخلیه آب های زیر زمینی به زون خاک، انجام شد. تخلیه آب های زیر زمینی به زون خاک شامل نفوذ از زون خاک است اما این امر رد گردیده است، زیرا هیچ زون غیر اشباعی وجود ندارد. نتایج حاصل از تخلیه آب های زیر زمینی به زون خاک در این مقاله ارائه شده چرا که این تخلیه بخشی از بودجه آب های زیرزمینی است و به عنوان یک نتیجه از توزیع هدایت هیدرولیکی در لایه زیرسطحی در بخش زیرین زون خاک حاصل می شود.
هدایت هیدرولیکی عمودی و افقی (K) در زیر زون خاک بطور یکنواخت توسط یک دستور magnitude برای ایجاد یک پراکنش متوسط-K، و توسط دو دستور magnitude برای ایجاد یک پراکنش بالا-K افزایش یافته است. هدایت هیدرولیکی به پایین تر از مقادیر اولیه کاهش نمی یابند، زیرا مشخص شد که نتایج، به کاهش در مقدار K نسبت به افزایش در مقدار K بسیار کمتر حساس می باشند. شبیه سازی فرم ماندگار برای هر پراکنش K جهت ایجاد شرایط اولیه که به هر توزیعی از مقدار ویژه K مطابقت داده شد، اجرا گردید.
مجموع نرخ های نفوذ به منطقه غیر اشباع متناسب با افزایش K در زمان، هنگامی که مقدار رطوبت کل در داخل زون خاک به دلیل ذوب برف در فصل بهار بالا بود، افزایش یافته بود. مقدار آب در دسترس برای نفوذ به منطقه غیر اشباع در زیر زون خاک در طول ذوب برف در فصل بهار توسط مقداری از هدایت هیدرولیکی عمودی در زون غیر اشباع محدود شده بود (شکل 2). با این حال، مجموع نرخ های نفوذ به منطقه غیر اشباع به مقدار هدایت هیدرولیکی عمودی به دنبال ذوب برف در فصل بهار کمتر حساس بودند، چرا که نفوذ توسط آب قابل دسترس در زون خاک محدود شده بود (شکل 2).
نرخ تغذیه آب های زیر زمینی متناسب با افزایش هدایت هیدرولیکی افزایش نمی یابد. توزیع متوسط-K منجر به بزرگترین نرخ تغذیه در طول دوره ذوب برف شد (شکل 3). عمده ای از این تغذیه جایی که سطح آب در نزدیکی بستر زون خاک بود اتفاق افتاده است. حداکثر نرخ تغذیه برای مقادیر بالا و پایین-K دارای توزیع مشابه ای بود. این نتایج غیر منتظره را می توان به ضخامت زون غیر اشباع در زمان و میزان تغذیه، و همچنین به تغییرات در جریان های جانبی ناشی از افزایش هدایت هیدرولیکی افقی نسبت داد.
نرخ تغذیه بالاتر برای توزیع متوسط K در مقایسه با پراکنش K کم به دلیل وجود جریانات عمودی بیشتر، از طریق یک ضخامت مشابه در زون غیر اشباع هستند. نرخ تغذیه کمتر برای توزیع بالا-K در مقایسه با پراکنش متوسط-K بواسطه یک سطح آب بسیار پایین تر است، که باعث ایجاد ضخامت بیشتر در زون غیر اشباع که سبب تاخیر در تغذیه شد، گردید. این امر در نحوه و روش، به زهکشی آهسته از طریق یک منطقه با ضخامت کمتر اشباع شده برای توزیع کم-K شبیه است. علاوه بر این، پراکنش بالا-K اجازه داد تا آب بیشتری در زون غیر اشباع، که آب زیرزمینی را بسیار طولانی تر پس از ذوب برف در فصل بهار تغذیه کرد، نسبت به توزیع های K متوسط یا کم ذخیره گردد. سطح آب های زیر زمینی در مناطق مرتفع برای پراکنش K بالا عمیق ترین مقدار خود را داشتند؛ به این دلیل که آب زیرزمینی با سهولت بیشتری به آبراهه ها سرازیر شد. مناطق مرتفع نسبت بیشتری از مساحت حوضه ها را در مقایسه با مناطق دشت های دره، تشکیل می دهند؛ در نتیجه، تغییر در مقادیر K در این مناطق تا حد زیادی می تواند زمان و مقدار تغذیه در حوضه را تغییر دهد.
همچنین تخلیه آب های زیر زمینی به زون خاک به طور متناسب سبب افزایش هدایت هیدرولیکی نشد، و در کاراکتر با نرخ های تغذیه مشابه بود (شکل 4). بیشینه تخلیه آب های زیر زمینی برای توزیع متوسط K تنها در طول دوره ای از نفوذ زیاد بود، چرا که سطح آب بالاتر از بخش زیرین زون خاک در منطقه ای وسیع از حوضه قرار داشت. در نتیجه، تأخیر کمی بین نفوذ، تغذیه، و تخلیه آب های زیر زمینی در این مناطق وجود داشت. تخلیه آب های زیر زمینی به زون خاک برای توزیع بالا-K در یک مورد که ذوب برف متوقف گشت و زون خاک خشک گردید، بیشینه بود. تخلیه آب های زیر زمینی به دنبال ذوب برف در چند منطقه محدود گردید، در درجه اول در نزدیکی کف دره، برای هر سه توزیع K. بنابراین، مناطق موثر در تخلیه آب های زیر زمینی به دنبال ذوب برف برای هر سه توزیع K مشابه بودند، اگر چه مقدار تخلیه آب های زیر زمینی متناسب با افزایش هدایت هیدرولیکی افزایش یافته بود.
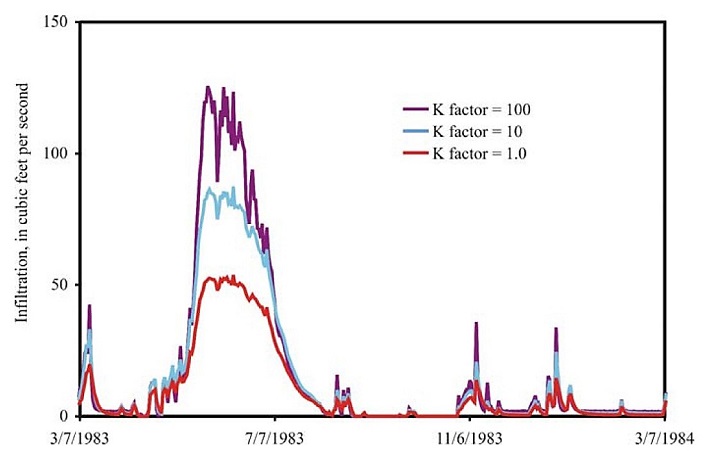
شکل 2. اثر هدایت هیدرولیکی زیرسطحی در مجموع نفوذ به منطقه غیر اشباع در زیر زون خاک.
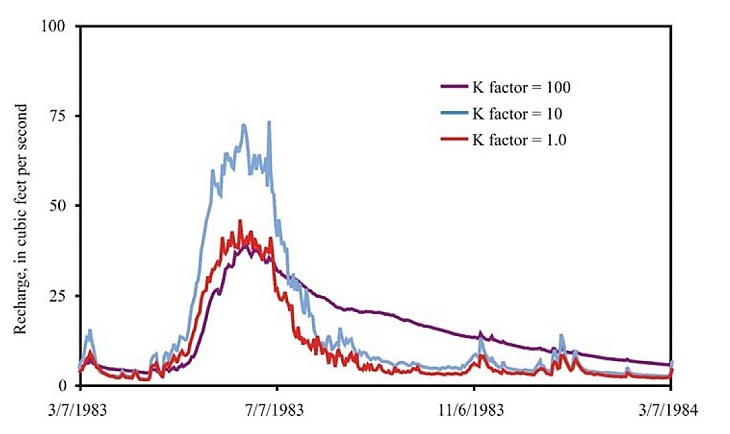
شکل 3. اثر هدایت هیدرولیکی زیرسطحی در تغذیه در کل.
 شکل 4. اثر هدایت هیدرولیکی زیرسطحی در مجموع تخلیه آب های زیر زمینی حوضه به زون خاک.
شکل 4. اثر هدایت هیدرولیکی زیرسطحی در مجموع تخلیه آب های زیر زمینی حوضه به زون خاک.
بحث و نتیجه گیری:
GSFLOW یک مدل بارش-رواناب و جریان آب های زیرزمینی جفت شده است که توازن توده های آب و نرخ تبادل آن را در میان مناطق مختلف، از جمله سطح زمین، زون خاک، مناطق زیرسطحی اشباع شده و غیر اشباع فراهم می کند. GSFLOW برای شبیه سازی جریان بارش، رواناب و آب های زیرزمینی جفت شده در نواحی بزرگ به دلیل آن که بر یک روش کارآمد برای شبیه سازی جریان مناطق غیر اشباع متکی می باشد، مناسب است. مدل های جفت شده جریان بارش-رواناب و آب های زیرزمینی که ترکیب کننده معادله 3-D ریچاردز برای شبیه سازی جریان در مناطق زیرسطحی می باشد؛ نیازمند شبکه سلولی بسیار کوچکتر و مراحل زمانی هستند، که این محدودیت برنامه های کاربردی، از جمله مدل سازی در مناطق نسبتا کوچک است. مبادلات در یک مدل ساده تر، این است که زون های غیر اشباع باید در جهت عمودی همگن بوده و شیب های مویین نادیده گرفته شوند. با این حال، معادله دقیق تر ممکن است دقت بیشتری را در هنگام مدل سازی جریان غیر اشباع در نواحی بزرگ به دلیل عدم قطعیت در بسیاری متغیرهای ورودی که مورد نیاز است، برای حل معادله D-3 ریچاردز ارائه ندهد. تجزیه و تحلیل حساسیت اثرات هدایت هیدرولیکی در زون زیر سطحی پایین تر از زون خاک در نفوذ، تغذیه، و تخلیه آب های زیر زمینی به زون خاک نشان داد که ضخامت زون غیر اشباع می تواند اثر قابل توجهی بر روی زمان بندی و نرخ تغذیه در حوضه Sagehen داشته باشد. این نتایج به احتمال زیاد به حوزه های دیگر که ارائه دهنده برجستگی های مهم، همانگونه که ضخامت زون غیر اشباع حساس به هدایت هیدرولیکی می باشد، تعمیم داده می شود. زمان و نرخ تغذیه، تغییرات در ذخیره سازی آب های زیر زمینی، و در نتیجه، در دسترس بودن آب برای جمعیت های انسانی و حیات وحش را تحت تاثیر قرار می دهند.
منابع:
Charbeneau, R.J. (1984). “Kinematic models for soil moisture and solute transport,” Water Resour. Res., 20(6), pp 699-706.
Colbeck, S.C. (1972). “A theory of water percolation in snow,” Journal of Glaciology, 2(63), pp 369-385.
Harbaugh, A.W., Banta, E.R., Hill, M.C., and McDonald, M.G. (2000). MODFLOW- 2000, the U.S. Geological Survey Modular Ground-Water Model-Modularization Concepts and the Ground-Water Flow Process. U.S. Geol. Survey Open-File Report 00-92.
Leavesley, G.H., Lichty, R.W., Troutman, B.M., and Saindon, L.G. (1983). Precipitation-Runoff Modeling System—User’s Manual. U.S. Geol. Survey Water-Res. Invest. Report 83-4238.
Leopold, L.B., Wolman, M.G., and Miller, J.P. (1992). Fluvial Processes in Geomorphology. Dover Publications, Inc. ,Mineola, New York.
Lighthill, M.J., and Whitham, G.B. (1955). “On kinematic waves—I, Flood movement in long rivers,” Proc. Royal Society London, Series A, 229, pp 281-316
Markstrom, S.L., Regan, R.S., Niswonger, R.G., Prudic, D.E., and Viger, R.J. (2006). “GSFLOW—A basin-scale model for coupled simulation of ground-water and surface-water flow—Part A. Concepts for modeling surface-water flow with the U.S. Geological Survey precipitation-runoff modeling system,” this issue.
McDonald, M.G., and Harbaugh, A.W. (1988). A Modular Three-Dimensional Finite-Difference Ground-Water
Flow Model. U.S. Geol. Survey Tech. of Water-Res. Invest., Bk 6, Chap. A1.
Niswonger, R.G., and Prudic, D.E. (2006). Documentation of the Streamflow-Routing (SFR2) Package to Include Unsaturated Flow Beneath Streams—a Modification to SFR1. U.S. Geol Survey Tech. and Meth., Bk 6, Chap. A13.
Niswonger, R.G., Prudic, D.E., and Regan, R.S. (in press). Documentation of the Unsaturated-Zone Flow (UZF1) Package for Modeling Percolation Between the Land Surface and the Water Table with MODFLOW. U.S. Geol. Survey Tech. and Meth., Bk 6, Chap. A19.
Panday, S., and Huyakorn, P.S. (2000). “A fully coupled physically-based spatially-distributed model for evaluating surface/subsurface flow,” Advances in Water Resources, 27, pp 361-382.
Pikul, M.F., Street, R.L., and Remson, I. (1974). “A numerical model based on coupled one-dimensional Richards' and Boussinesq equations,” Water Resour. Res., 10(2), pp 295-302.
Prudic, D.E., Konikow, L.F., and Banta, E.R. (2004). A New Streamflow-Routing (SFR1) Package to Simulate Stream-Aquifer Interactions with MODFLOW-2000. U.S. Geol. Survey Open-File Report 2004-1042.
Refsgaard, J.C., and Storm, B. (1995). MIKE SHE, in Singh, V.P., ed., Computer Models of Watershed Hydrology. Highlands Ranch, Colo., Water Res. Pub., pp 809-846.
Smith, R.E. (1983). “Approximate sediment water movement by kinematic characteristics,” Soil Science Soc. of Am. Journal, 47, pp 3-8.
Thoms, R.B., Johnson, R.L., and Healy, R.W. (in press). User’s Guide to the Variably-Saturated Flow (VSF) Process for MODFLOW. U.S. Geol. Survey Tech. and Meth., Bk 6, Chap. A18.. 6, Chap. A18
___________________________________
این متن ترجمه ای بود از مقاله ای که در ذیل قادر به دریافت آن می باشید. همچنین فایل PDF ترجمه به سبب بهم ریختگی نسبی فرمول های متن آن در صفحات اینترنتی، در ادامه قابل دانلود می باشد.




مدیر سایت: بهزاد سرهادی کارشناس ارشد مهندسی آب
شناسه تلگرام مدیر سایت: SubBasin@
نشانی ایمیل: behzadsarhadi@gmail.com
(سوالات تخصصی را در گروه تلگرام ارسال کنید)
_______________________________________________________
پروژه تخصصی در لینکدین









 در منابع آب
در منابع آب





































نظرات (۰)