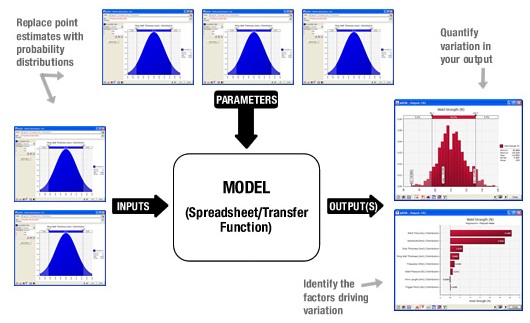
روش مونت کارلو یک روش مرسوم برای آنالیز عدم قطعیت در مدل های عددی پیچیده است. این روش یک روش استوکستیک است و به کار گیری آن منوط به داشتن اطلاعات کافی در مورد دانش متغیرهای تصادفی و روش استوکستیک می باشد. در این روش فرض می شود که هر پارامتر ورودی در مشاهدات و اندازه گیری ها یک متغیر تصادفی است که دارای یک تابع توزیع احتمال و یک تابع تجمعی احتمال می باشد (شکل را مشاهده کنید) الگوریتم روش مونت کارلو در شکل زیر نشان داده شده است.

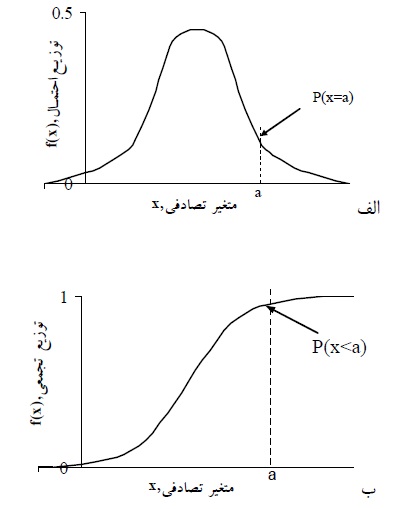
الف: تابع توزیع احتمال، ب: تابع توزیع تجمعی برای یک متغیر تصادفی

گام اول در تحلیل این روش این است که تابع توزیع احتمال یا تابع تجمعی احتمال برای متغیرهای ورودی فرض و یا با توجه به اندازه گیری ها تعیین شود. تابع های توزیع احتمال معمول در مطالعات هیدرولوژیکی شامل توزیع نرمال، لگاریتمی نرمال، نمایی، یکنواخت، مثلثی، پواسن و بتا می باشد. توزیع بعضی از پارامترها مانند هدایت هیدرولیکی معمولا لگاریتمی نرمال فرض می شود و توزیع بعضی دیگر از پارامترها مانند تخلخل معمولا نرمال فرض می شود.

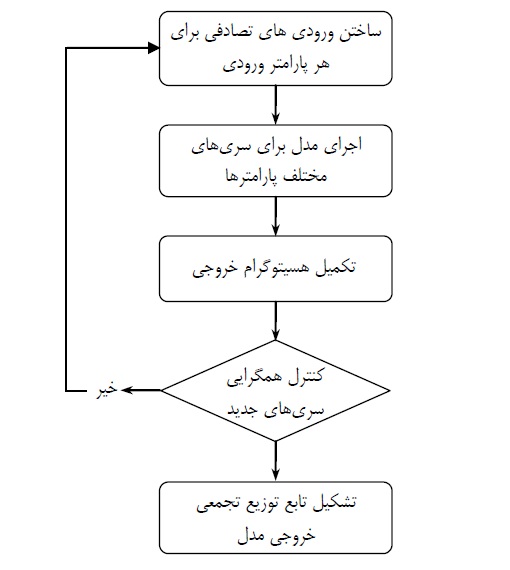
الگوریتم آنالیز به روش مونت کارلو

گام دوم این است که مقدار هر پارامتر ورودی مستقل، به صورت تصادفی و با توجه به تابع توزیع احتمال تعیین شود. به این منظور به کمک یک مولد عدد تصادفی برای هر پارامتر یک عدد بین 0 و 1 انتخاب میشود و سپس این عدد به کمک تابع توزیع احتمال و با توجه به میانگین و واریانس آن به مقدار احتمالی پارامتر تبدیل می شود. پس از تعیین یک سری پارامتر ورودی به صورت احتمالی این مرحله به دفعات (مثلا 50 بار) تکرار می شود تا سری های مختلفی از پارامتر ورودی آماده شود. گام بعد این است که به کمک هر سری پارامتر ورودی یک بار مدل اجرا شود و نتایج تعیین شود.

در گام چهارم نمودار هیستوگرام داده های خروجی پس از هر بار شبیه سازی، بازسازی و رسم می شود و تعداد نتایج در هر محدوده مشخص می شود. به این ترتیب تابع توزیع احتمال تعیین می شود. در گام پنجم همگرایی تابع احتمال کنترل می شود. به منظور کنترل همگرایی سری های جدیدی از پارامترهای ورودی انتخاب شده و پس از تحلیل، تابع توزیع جدیدی رسم می شود. در صورتی که اختلاف بین دو نمودار قابل توجه باشد، آنالیز همگرا نشده است و باید نمودار جدیدی به کمک کل نتایج تحلیل رسم شود و دوباره از گام دوم به بعد تکرار شود تا اطمینان حاصل شود همگرایی صورت گرفته است. پس از اطمینان از همگرایی، تابع تجمعی احتمال خروجی تعیین می شود. به کمک این تابع، می توان ریسک انتخاب یک مقدار را به عنوان نتیجه مدل سازی تعیین نمود.

موارد ویژه ارزیابی عدم قطعیت درمدل های آب زیرزمینی

عدم قطعیت در آبدهی مجاز

آبدهی مجاز مقدار بده قابل برداشت از آبخوان است که باعث تغییرات غیر قابل قبول در شرایط هیدرولیکی و زیست محیطی نمی شود و بستگی به میزان میانگین تغذیه درازمدت آبخوان دارد. میانگین تغذیه دراز مدت معمولا به طول زمان میانگین گیری و شروع آن حساس است. به منظور کاهش عدم قطعیت در میانگین تغذیه درازمدت، پس از تعیین یک دوره حداقل قابل قبول برای میانگین گیری، برای تمام دوره های ممکن که اطلاعات وجود دارد میانگین گیری صورت می گیرد و نتایج حاصله مرتب شده و احتمال وقوع حالات مختلف تعیین شده و تابع توزیع احتمال رسم می شود.

تابع توزیع، این دید را می دهد که انتخاب یک مقدار تغذیه میانگین سالانه و آبدهی مجاز برای آبخوان با چه ریسکی همراه است. محدودیت اصلی این روش انتخاب طول زمان میانگین گیری مناسب است. ویژگی اصلی روش این است که برای هر آبدهی مجاز، عدم قطعیت آن را به صورت کمی بیان می کند.

عدم قطعیت در تنش های سامانه

تعیین عدم قطعیت در پیش بینی های مدل، با بررسی نتایج پس از تکمیل زمان شبیه سازی و مقایسه پیش بینی های مدل با آنچه در واقعیت رخ داده امکان پذیر است. ممکن است نتایج پی شبینی با واقعیت اختلاف داشته باشد. یکی از دلایل این اختلاف عدم همخوانی تنش های اعمال شده به مدل با آنچه در واقعیت اتفاق افتاده است، می باشد.

الف- روش های کاهش عدم قطعیت در تنش های سامانه

- یکی از روش های کاهش عدم قطعیت ناشی از تنش های اعمال شده به مدل این است که شبیه سازی در محدوده وسیعی از حالت های مختلف تنش ها انجام گیرد. با این روش محدوده های مختلفی از پاسخ آبخوان نشان داده خواهد شد، ولی احتمال وقوع هر حالت را نمی توان به صورت کمی بیان کرد.

- یک روش دیگر استفاده از تحلیل مونت کارلو روی تنش های سامانه می باشد. در روش مونت کارلو همان طور که پیش تر ارائه شد، مقدار هر تنش از یک تابع توزیع احتمالی فرض شده یا اندازه گیری شده به صورت تصادفی انتخاب می شود. اعمال این روش در مدل های عددی خیلی پیچیده که تنش ها تابع زمان و مکان هستند، بسیار مشکل است.

- یک روش عملی تر انتخاب پارامترها به صورت تصادفی از سری های زمانی است. به عنوان مثال فرض شود در یک شبیه سازی دوره زمانی تنش ها یک ماه است. مدت زمان شبیه سازی 36 ماه و ماه شروع شبیه سازی فروردین است و برای 30 سال اطلاعات موجود است. برای به دست آوردن اطلاعات فروردین اولین سال شبیه سازی، به طور تصادفی یک عدد از بین 1 تا 30 انتخاب می شود و اطلاعات فروردین آن سال مورد استفاده قرار می گیرد. سپس یک عدد تصادفی دیگر انتخاب می شود و اطلاعات اردیبهشت آن سال مورد استفاده قرار می گیرد و این روند ادامه پیدا می کند تا شبیه سازی تکمیل شود. تحلیل به دفعات (مثلا 100 بار ) با ورودی های مختلف صورت می گیرد و در هر حالت نتایج تعیین می شود. سپس نتایج مرتب می شوند و برای هر شاخص تابع های توزیع تجمعی رسم می شود. به کمک این تا بع ها می توان احتمال وقوع هر پی آمد را به صورت کمی بیان کرد. برای مدل های پیچیده در این روش باید تعداد اجراها بیش تر شود.

ب- شبیه سازی های طولانی

اگر زمان شبی هسازی طولانی باشد (مثلا بیش از 10 سال) یک پیش بینی ماندگار به کمک روش مون تکارلو مناسب تر است. در این حالت اثر عدم قطعیت در تنش ها را م یتوان به کمک تحلیل های مختلف در حالت های خشک، متوسط و مرطوب بررسی کرد. برای تحلیل در سه حالت فوق بهتر است تنش ها از تابع های توزیع تجمعی دراز مدت و با توجه به احتمال های 20، 50 و 80 درصد تعیین شوند. با توجه به پاسخ سامانه ممکن است روش ناماندگار پیش بینی مناسب تری از روش ماندگار بدهد.

مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

پروژه تخصصی در لینکدین

×

 براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح