2.2 طوفان طراحی حاصل از منحنی های IDF

1.2.2 بارندگی توزیع یکنواخت زمان

بارندگی با توزیع زمان یکنواخت با یک شدت ثابت در طول مدت آن مشخص می شود، که برابر با زمان تمرکز حوضه برای مناطق کوچک در نظر گرفته شده است. شدت با فرمول کلی زیر محاسبه می شود:

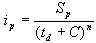
جایی که:

• S_p پارامتر وابسته به مکان و احتمال بیش از حد p است. برای p مشخص (معمولاً برای p = 1٪) مقدار Sp به صورت خطوط هم مقدار که روی نقشه ترسیم شده اند، داده می شود. به عنوان مثال، نقشه با خطوط هم مقدار پارامتر S_1% مشتق شده توسط Platageaدر سال (1966) برای قلمرو رومانی در شکل 2.1 ارائه شده است.
•  C پارامتر که می تواند به صورت جانبی گرایش شدت را ایجاد کند در حالی که مدت زمان t_d بسیار کوچک می شود (به عنوان مثال برای مناطق حوضه های بسیار کوچک زیر 1 کیلومتر مربع).
•  t_d مدت زمان است.
•  n پارامتری که بین 0.5-0.67 متفاوت است. نقشه رومانی با خطوط هم مقدار n در شکل 2.2 نشان داده شده است.

کاربردی از فرمول حاضر در مطالعات Drobot and Serban در سال (1999) آورده شده است.

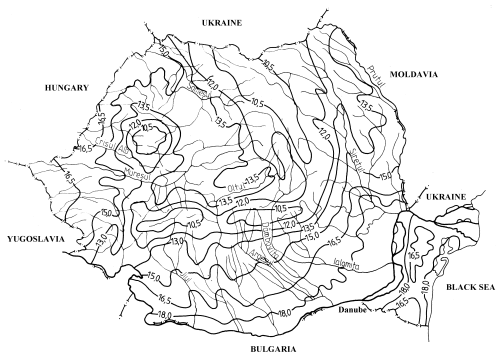
شکل 1.2 خطوط هم مقدار پارامتر S_1%.

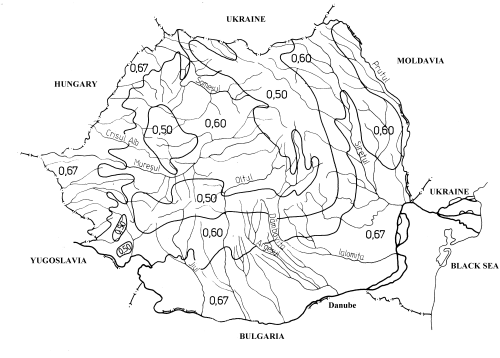
شکل 2.2 خطوط هم مقدار پارامتر n.

در حالی که از فرمول منطقی استفاده می شود، فرض توزیع ثابت زمان شدت طوفان طراحی منجر به دست کم گرفتن تخلیه اوج طراحی می شود، به ویژه برای مناطق و حوضه های با مساحت بیش از 5-10 کیلومتر مربع. به عنوان مثال، در منطقه لیون (Musy, 1998) احتمال وجود دو نیمه باران در مدت زمان 60 دقیقه فقط 5٪ است. حتی در این حالت توزیع یکنواخت شدت اثبات نمی شود. توزیع متوسط برای دو نیمه از عمق 60 دقیقه بارندگی به ترتیب 74 و 26 درصد است.

2.2.2 طوفان مرکب

مفهوم طوفان مرکب از طوفان یکنواخت به واقعیت نزدیکتر است. وقوع طوفان مرکب نیز بر اساس منحنی IDF است. فرضیه اصلی طوفان ترکیبی این است که حداکثر شدت هایی که در طول مدت معین به طور متوسط ​​انجام می شوند، همان هایی است که از منحنی های IDF بدست می آید. مراحل محاسبه به شرح زیر است:

• اول از همه، کل مدت طوفان طراحی تعیین می شود.
• برای یک احتمال خاص بیش از حد p (فرکانس) و مدت زمان بارندگی t_d (مربوط به زمان تمرکز حوضه) برآورد طوفان شدت متوسط ​​با معادله بالا تعیین می شود.
• کل مدت t_d در فواصل زمانی جزئی t₁, t₂ = t₁ + Δt, t₃ = t₂ + Δt… t_n = t_n-1 + Δt, تقسیم می شود، جایی که Δt (دقیقه) یک مرحله زمانی ثابت است. برای تمام مقادیر مدت جمع شده t₁, t₂, t₃… t_n شدت متوسط 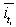 ​​با استفاده از همان رابطه حاضر ارزیابی می شود.
• سپس برای فواصل زمانی t₁, t₂, t₃… t_n عمق تجمع باران با استفاده از رابطه حاصل می شود:

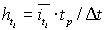
• در حال حرکت به جلو (فروارد)، عمق بارندگی برای هر مرحله زمانی به عنوان تفاوت بین مقادیر دو عمق طوفان تجمع یافته بعدی مربوط به هر بازه زمانی تعیین می شود و سپس شدت طوفان برای هر دهانه زمان مانند شکل 3.2 نشان داده شده است، رابطه:

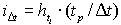
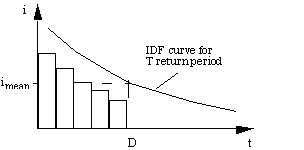
شکل 3.2 ساخت طوفان مرکب.

• نمودار کاهش شدت (شکل 3.2) ممکن است با قرار دادن حداکثر شدت در مرکز مدت طوفان "مرتب شود" همانطور که ​​در شکل 4.2 نشان داده شده است.

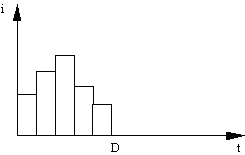
شکل 4.2 طوفان طراحی بر اساس روش طوفان مرکب.

3.2.2 روش دنباله بحرانی بارندگی

این روش که در سال 1965 توسط ایالات متحده به دست آمد، فرض بارش 4 روزه شرکت کننده در تشکیل سیل را در نظر می گیرد. توالی بحرانی با افزایش تدریجی شدت بارندگی طی چهار روز در نظر گرفته شده، به روشی تعریف می شود، به گونه ای که در آغاز طوفان سیلاب، خاک در رطوبت قابل توجهی قرار گیرد. چنین توزیع زمانی بارندگی منجر به حداکثر رساندن حجم سیل و اوج تخلیه می شود زیرا طوفان محرک بر روی خاک مرطوب سقوط می کند و از این رو نفوذ نفوذ ناچیز خواهد بود. در جدول 2.1 مراحل محاسبه به عنوان مثال ارائه شده است به شرح زیر [Stanescu, 1995]:

• برای چندین برآورد استاندارد از مدت زمان بارندگی و یک دوره بازگشت خاص تصویب شده T، عمق بارش با استفاده از منحنی IDF تعیین می شود. مقادیر استاندارد مدت زمان 1، 2، 3، 4، 5، 6، 12، 18، 24، 48، 72 و 96 ساعت (4 روز) است.
• در جدول 2.2 عمق بارندگی برای مقادیر استاندارد طول مدت و برای فرکانس های 1/2 ، 1/10 و 1/100 سال ارائه شده است.

جدول 1.2 عمق باران (میلی متر) در مقادیر مختلف استاندارد طول طوفان.

Standard duration D (hours)	Frequency (years)
	1/2	1/10	1/100
1	50	67.5	95
2	65	87.5	125
3	72	100	145
4	80	107.5	157.5
5	82.5	115	167.5
6	85	120	175
12	100	140	205
18	107.5	150	222.5
24	112.5	157.5	235
48	132.5	190	285
72	145	210	317
96	157.5	225	342.5
Time interval (hours)	Hourly rainfall distribution over 6 hour-duration
0-1	50	67.5	95
1-2	15	20	30
2-3	7.5	12.5	20
3-4	7.5	7.5	12.5
4-5	2.5	7.5	10
5-6	2.5	5.0	7.5
Time interval (hours)	6 hour-distribution over 24 hour-duration
0-6	85	120	175
6-12	15	20	30
12-18	7.5	10	17.5
18-24	5.0	7.5	12.5
Time interval (hours)	24 hour-distribution over four days
0-24	112.5	157.5	235
24-48	20	37.5	50
48-72	12.5	20.0	32
72-96	12.5	15	25.5

• در طول 6 ساعت زمان، توزیع ساعتی عمق (یا شدت) با تمایز مقادیر بعدی عمق بارندگی بدست می آید. به طور مشابه، توزیع 6 ساعته در بازه زمانی 24 ساعته و توزیع 24 ساعته در طول سه روز باقیمانده ارزیابی می شود.
• توزیع زمان عمق باران از شدت مربوط به روز اول فاصله 72-96 و سپس به فواصل 48-72 و 24-48 ساعت (یعنی به ترتیب معکوس) محاسبه می شود.
• سپس برای 3 روز اول عمق بارندگی 15، 20 و 32.5 میلی متر است. روز چهارم در سه دوره 6 ساعته با عمق های 7.5، 10 و 20 میلی متر تقسیم می شود. در طول آخرین دوره 6 ساعته، عمق طوفان به صورت ساعتی 5، 7.5، 7.5، 12.5، 20 و 67.5 میلی متر توزیع می شود. توزیع زمان در فواصل زمانی 6 ساعت، 24 ساعت و سه روز برای فرکانس 1/10 سال در جدول 2.2 نشان داده شده است و کاتالیست باران طراحی در شکل 5.2 ارائه شده است.

جدول 2.2 توزیع زمان عمق بارندگی.

Time interval (hours)	Time distribution of the rainfall depth - h (mm)			Total depth (mm)
	3 days	6 hours	1 hours
96-72	15			15
72-48	20			35
48-24	32.5			67.5
24-18		7.5		75
18-12		10		85
12-6		20		105
6-5			5.0	110
5-4			7.5	117.5
4-3			7.5	125
3-2			12.5	137.5
2-1			20.0	157.5
1-0			67.5	225

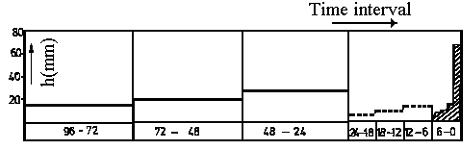
شکل 5.2. هایتوگرافی طوفان طراحی با مدت زمان 4 روز.

می توان مشاهده کرد که بارندگی در 3 روز اول و حتی در سه دوره 6 ساعته اول به خیس شدن خاک کمک می کند در حالی که طوفان توزیعی یک ساعته دوره چهارم منجر به رواناب حداکثر می شود. در این مثال زمان تمرکز یک ساعت در نظر گرفته شده است. اگر اندازه حوضه متضمن زمان متغیر متفاوتی باشد، آخرین دوره 6 ساعته به چنین روشی به پارتیشن تقسیم می شود، حداقل آخرین بازه زمانی باید با زمان تمرکز مطابقت داشته باشد.

4.2.2 طوفان طراحی "نوع شیکاگو"

این روش (Keifer and Chu, 1957) تعیین یک hyetograph مصنوعی را می توان از رابطه تجربی منحنی IDF شروع کرد. بیایید فرم کلی فرمول Talbot IDF را در نظر بگیریم:

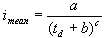
جایی که:

•  i_mean شدت متوسط در طول طوفان.
•  a, b, c عملکرد پارامترهایی از مکان و فرکانس

نقل قول:

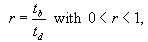
کجا: t_b زمان قبل از بالاترین شدت باران (دقیقه) است

و:

t_d = t_b + t_a

که t_b مدت زمان طوفان است که لحظه حداکثر شدت را دنبال می کند.

از معادلات بالا می توان نتیجه گرفت:

t_b = r · t_d

و:

t_a = (1 - r) · t_d

جایی که t_b در سمت چپ قله طوفان اندازه گیری می شود در حالی که t_a در سمت راست حداکثر مقدار طوفان اندازه گیری می شود همانطور که در شکل 6.2 نشان داده شده است.

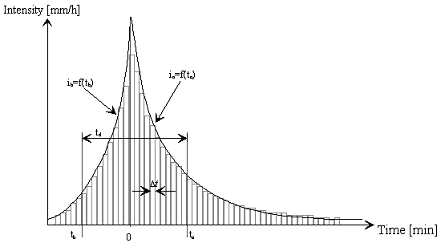
شکل 6.2 ساخت هایتوگرافی از نوع شیکاگو.

از آنجا که شدت آن به مدت زمان بستگی دارد، فرد در نظر می گیرد: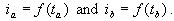 

سپس، طوفان کل در طول مدت زمان نوشته شده است:

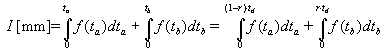
این عبارت امکان تعیین شدت طوفان را برای فواصل زمانی مختلف قبل و بعد از حداکثر مقدار فراهم می کند. با توجه به اینکه 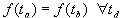 می توان نوشت:

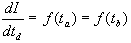
از طرف دیگر طوفان کل I = i_mean · t_d است و بنابراین:

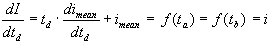
با توجه به روابط حاضر می توان مقادیر i, i_a و i_b را تعیین کرد، به شرح زیر:

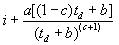
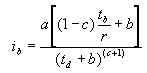
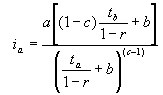
موقعیت شدت اوج در hyetograph به شرح زیر تعیین می شود:

ضریب r شکل hyetograph را از نظر موقعیت قله مشخص می کند. ضریب r با پردازش هایتوگرافی ثبت شده طوفان ها با در نظر گرفتن چندین مقدار  t_r از طول باران شدید در مجاورت قله طوفان و محاسبه میانگین مقدار (r(t_r مشاهده شده برای همه طوفان های ثبت شده تعیین شده، تعیین می شود. سپس مقدار نهایی با استفاده از وزنه های t_r بدست می آید، بدین ترتیب:

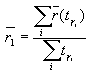
چندین محقق برخی از مقادیر r را برای طوفان در مکان های مختلف تجزیه و تحلیل کرده اند. این مقادیر به شکلی نزدیک به یکدیگر هستند که در جدول 3.2 نشان داده شده است.

جدول 3.2 مقادیر r برای طوفان نوع شیکاگو.

Location	r	Source
Baltimore (1958)	0.399	Mc. Pherson
Chicago (1957)	0.375	Keifer and Chu
Cincinnati (1973)	0.325	Preul and al.
Ontario (1978)	0.488	Marsalek
Philadelphia (195x)	0.414	Mc. Pherson

طبق نظر Debordes در سال (1974) ضریب r به طور مساوی در فاصله (0، 1) توزیع می شود به طوری که محتمل ترین مقدار نزدیک به مقدار 0.5 یافت می شود. تا آنجا که تأثیر موقعیت قله طوفان وجود دارد، Debordes و Raous در سال (1976) نشان داده اند که بالاترین میزان تخلیه قله با فرض همان حجم طوفان برای قله های تأخیر، یعنی r بزرگتر از 0.5 و کوچکتر از 1 بدست می آید. واقعیت واضح است، زیرا نفوذ در حالت قرار دادن اوج طوفان در نیمه اول مدت بارش (r بزرگتر از 0.5 و کوچکتر از 1) بیشتر است، همانطور که در شکل 7.2 نشان داده شده است. Serban و Balut در سال (1975) بسیاری از وقایع طوفان در رومانی را مورد تجزیه و تحلیل قرار دادند و آنها نتیجه گرفتند که دو نوع باران شدید وجود دارد: یکی عدم تقارن مثبت با جبهه های سرد و مسدود و دیگری با عدم تقارن منفی با جبهه های گرم یا ثانویه. نوع دوم توزیع مربوط به میزان بارندگی ضعیف تری نسبت به طوفان های نوع اول است که از جبهه های سرد و خاموش منشا می گیرند. نسبت بین حجم کل و حجم بارانی که می بارد تا زمان ثبت شدت اوج در شکل 8.2 ارائه شده است.

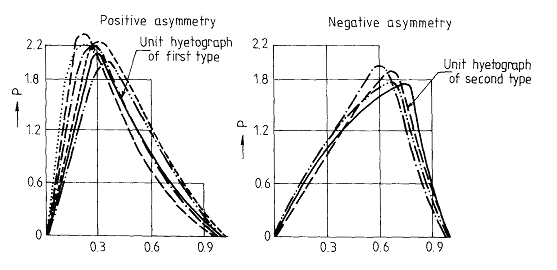
شکل 7.2 دو نوع بارندگی شدید.

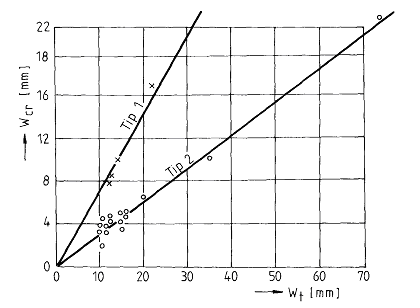
شکل 8.2 نسبت بین حجم کل و حداکثر حجم طوفان.

مراحل زیر در حین استفاده از روش شیکاگو انجام می شود:

یک فاصله زمانی Δt و موقعیت قله طوفان را که توسط r داده شده است انتخاب کنید.

برای Δt انتخاب شده شدت پیک (حداکثر) را از فرمول محاسبه کنید:

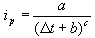
i_p شدت پیک را در اطراف قله توزیع کنید تا روابط  r.Δt قبل از اوج و:

(1-r).Δt 

مشخص باشد.

سپس شدت باران در شاخه سمت راست هیاتوگراف با استفاده از رابطه ارزیابی می شود:

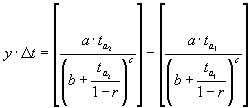
 جایی که:

•  y شدت باران بین نقاط t_a1 و t_a2؛
•  t_a1 زمان که مربوط به آغاز فاصله زمانی Δt اندازه گیری شده از اوج لحظه است (t = 0) ؛
•  t_a2 زمان که مربوط به پایان فاصله زمانی است: t_a2 = t_a1 + Δt

شدت باران در شاخه سمت چپ hyetograph با استفاده از رابطه ارزیابی می شود:

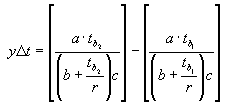
 جایی که:

•  t_b1 زمان مربوط به آغاز فاصله زمانی به سمت چپ، اندازه گیری شده از اوج لحظه (t = 0) ؛
•  t_b2 زمان که مربوط به پایان فاصله زمانی است: t_b1 = t_b1 + Δt.

روش شیکاگو در مواردی توصیه می شود که یک رویداد بسیار کوتاه باران باید مورد توجه قرار گیرد، به عنوان مثال طراحی شبکه فاضلاب یا هیدرولوژی سدهای بزرگ (Musy, 1998)

ویدیو آموزش فارسی نحوه محاسبه سیل طراحی سد - IDF

مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

پروژه تخصصی در لینکدین

×

 براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح