4.6 حل عددی مدلهای مسیریابی توزیع شده

معادلات Saint-Vénant معادلات دیفرانسیل جزئی هستند که به طور کلی باید با روش های عددی حل شوند. این روش ها را می توان روی معادلات اصلی سنت ونانت یا برای حل مجموعه ای از معادلات تبدیل شده ریاضی، که فرم مشخص معادلات سن ونت نامیده می شود، به کار برد. به عنوان مثال، جفت V-h (6.17) معادل فرم مشخص است:

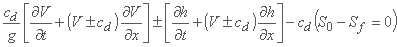
در هر نوع، بسیاری از روش های تفاوت محدود در دسترس هستند، اما فرم مشخصه نیز ممکن است توسط برخی از روش های مشخص درمان شود.

دسته آخر از این واقعیت سوits استفاده می کند که می توان دو معادله دیفرانسیل جزئی را با دو جفت معادله دیفرانسیل معمولی به شرح زیر جایگزین کرد:

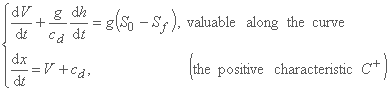
و

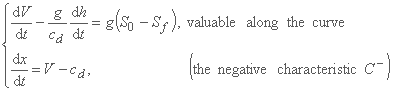
(6.28)

متغیرهای جریان V(x,t) و h(x,t) را می توان با ادغام اولین معادله هر جفت، در امتداد منحنی مشخصه مربوط به صفحه x-t، پیدا کرد. شرح مفصلی از روشهای مشخصه را می توان در Popa (1997) یافت.

در روشهای تفاضل محدود، محاسبات بر روی شبکه ای که از طریق دامنه جریان جالب به صفحه x-t قرار داده شده انجام می شود. این شبکه محاسباتی به ترتیب با برخی از مراحل مساوی یا متغیر به ترتیب Δx و Δt تعریف می شود. بنابراین شبکه ای از نقاط گسسته بدست می آید و متغیرهای جریان Q, z (or Q, h; V, z; V, h) فقط برای این تعداد محدود از نقاط شبکه مشتق می شوند. شکل 2.6 یک شبکه محاسباتی معمولی را نشان می دهد. موقعیت های مکانی نقاط شبکه با شاخص j و لحظه های زمانی با شاخص i نشان داده می شوند.

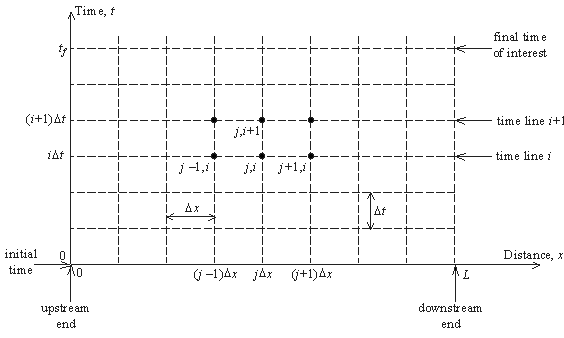
شکل 2.6 شبکه محاسباتی با ساختار تفاضل محدود.

به عنوان اصل، روش های تفاضل محدود حاکم بر معادلات دیفرانسیل جزئی را به مجموعه ای از معادلات تفاضل محدود جبری (خطی یا غیرخطی) تبدیل می کنند که برای اجازه دادن به مقادیر متغیرهای جریان در یک نقطه شبکه یا در تمام نقاط شبکه در یک خط زمان حل شده است . این معادلات تفاضل محدود با تقریب مشتقات زمان و مکان با برخی از عبارات تفاضل محدود بدست می آیند. نه تنها مشتقات، بلکه سایر اصطلاحات معادلات سن ونت نیز باید به روشی خاص تعریف شوند.

در مورد مشتق فضایی یک تابع مداوم f(x,t) در زمان لحظه ti و فضای xj روی شبکه در شکل 2.6، این را می توان به صورت تقریبی بدست آورد:

 تقریب تفاضل رو به جلو  ؛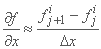

 یک رابطه تفاوت رو به عقب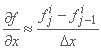 

 یک تفاوت اصلی  ،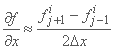

که در آن f_jⁱ مقدار f را در نقطه شبکه نشان می دهد (x_j ,t_i).

به روشی مشابه، مشتق زمان ممکن است به چندین روش مختلف تعریف شود، به عنوان مثال:

; 

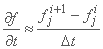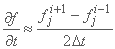
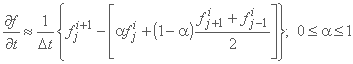
معمولاً مقدار تابع f(x,t) در نقطه شبکه (x_j,t_i) به عنوان f_jⁱ پذیرفته می شود، اما در مورد تقریب های مختلف نیز می توان تصمیم گرفت.

یک روش تفاوت محدود باید نوع خاصی از طرح تفاوت محدود را به کار گیرد. این طرح ها در دو کلاس عمده گروه بندی می شوند: طرح های تفاوت محدود و آشکار.

طرح های صریح به مواردی گفته می شود که در آن متغیرهای جریان در هر نقطه j و سطح زمانی i + 1 ممکن است فقط با استفاده از داده های شناخته شده در چند نقطه مجاور در خط زمانی i محاسبه شوند. این طرح ها به یک سیستم معادلات جبری منجر نمی شوند، بلکه فقط به دو معادله تفاضل محدود برای هر نقطه شبکه (x_j,t_i+1) منجر می شوند. با حل دو معادله، مقادیر ناشناخته متغیرهای جریان بدست آمده و سپس، محاسبه به نقطه شبکه بعدی در امتداد خط زمانی i + 1 می رسد.

در طرح های ضمنی، عبارات با تفاضل محدود برای تقریب فضا و / یا مشتقات زمان در نقطه شبکه (x_j,t_i+1) استفاده می شوند، شامل مقادیر ناشناخته متغیرهای جریان در چند نقطه مجاور در خط زمانی i + 1 هستند. در نتیجه، یک سیستم معادلات جبری برای یک خط زمانی معین i + 1 تولید می شود و با حل این سیستم، تمام مقادیر ناشناخته به طور همزمان در سطح زمانی i + 1 تعیین می شوند.

جایگزینی مشکل اصلی مداوم با یکپارچه سازی بر روی یک شبکه محاسباتی گسسته، خطاهای عددی را در نتایج وارد می کند. اگر چنین خطاهایی در حین محاسبه از یک سطح زمانی به مرتبه دیگر تقویت نشوند، یک طرح تفاضل محدود پایدار است. پایداری عددی به اندازه مراحل و زمان و مکان و برخی از خصوصیات جریان بستگی دارد. شرایط Courant:

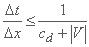
شرط لازم اما ناکافی برای پایداری یک طرح صریح است.

بنابراین، هر طرح صریحی به طور شرطی پایدار است، شرایط حاضر نیاز به کار با مراحل زمان کوچک در مقایسه با تکامل پدیده های فیزیکی دارد. علیرغم سادگی محاسباتی، به صراحت به دلایل این محدودیت پایداری از روشهای صریح در مدل سازی رودخانه استفاده می شود.

از طرف دیگر، طرح های ضمنی ممکن است پیچیده تر به نظر برسند، اما به طور کلی می توان آنها را بدون قید و شرط برای مراحل محاسبات بزرگ و با اندکی از دست دادن دقت پایدار کرد.

تمایز دیگر در میان طرح های مربوط به همان کلاس مربوط به نحوه تفکیک اصطلاحات غیر مشتق (مانند S_f(Q,h), B(h), A(h) و غیره) است. از آنجا که این اصطلاحات توابع متغیرهای وابسته هستند ، درمان آنها یک ویژگی خطی یا غیرخطی از معادلات تفاضل محدود را القا می کند.

بسیاری از طرح های تفاوت محدود با جزئیات بیشتر در بخشهای بعدی ارائه خواهد شد.

مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

پروژه تخصصی در لینکدین

×

 براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح