مجموعه آموزش هیدرولوژی - طرح تفاضل محدود برای مدل موج پویا

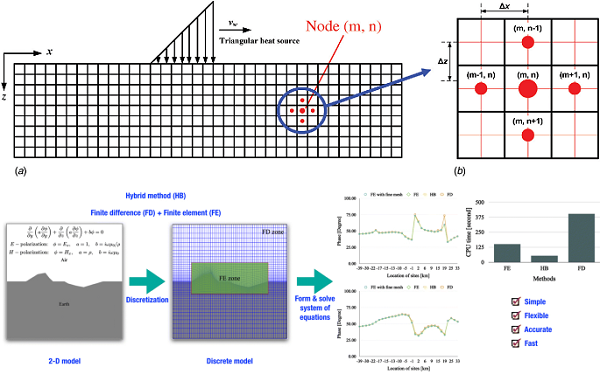
۲۰ بهمن ۹۹ ، ۱۹:۳۳ نويسنده: بهزاد سرهادی

5.6 طرح تفاضل محدود برای مدل موج پویا

ساده ترین طرح صریح مشتقات جزئی را در نقطه شبکه (x_j,t_i+1) از نظر مقادیر در نقاط مجاور (x_j-1,t_i), (x_j,t_i) و (x_j+1,t_i) تقریب می زند (شکل 3.6 ) به شرح زیر است:

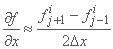
که در آن f ≡ Q (or V), z (or h)، و غیره

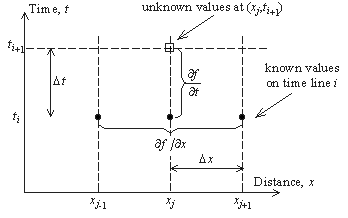
شکل 3.6 تقریب مشتق به ساده ترین طرح صریح.

با این حال، هر مشکل خاص نیاز به توضیحات بیشتری دارد.

جفت Q-h معادلات Saint-Vénant را در نظر بگیرید که ممکن است به صورت زیر نیز نوشته شود:

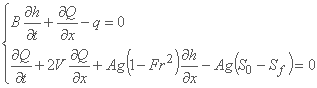
جایی که:

Fr شماره فرود محلی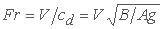

S_f بیان شده توسط معادله Manning 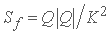, با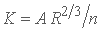

با استفاده از نمادها:

; ;( ),

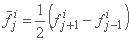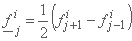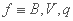و تقریبهای تفاضل محدود زیر:

;;;

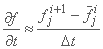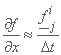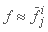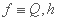
دو معادله اختلاف محدود مربوط به معادله حاضر به صورت زیر بدست می آیند:

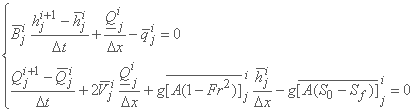
معادله اول یک رابطه صریح را برای مقدار ناشناخته h_jⁱ⁺¹ و رابطه دوم را برای مقدار ناشناخته Q_jⁱ⁺¹، یعنی:

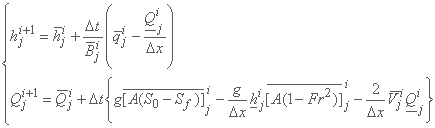
در انتهای مرز، از اشکال مشخصه استفاده می شود. برای معادلات سنت ونت، این موارد به شرح زیر است:

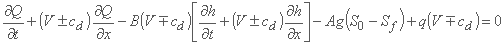
در معادله علامت برتر عمل می کند که در انتهای پایین دست اعمال می شود و با برخی عبارات تفاضل محدود به عقب تقریب می یابد، در حالی که معادله با علامت نازل در انتهای بالادست ارزشمند است و گسسته سازی آن به دنبال تفاضل محدود است.

برای مرز بالادست، یکی بدست می آورد:

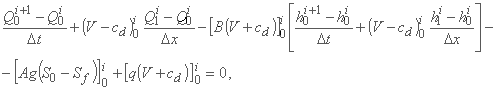
که باید با یک رابطه مکمل بین دو متغیر ناشناخته Q₀ⁱ⁺¹ و h₀ⁱ⁺¹ تکمیل شود (معمولاً هیدروگراف ورودی Q₀ = f_u(tⁱ⁺¹)).

در مرز پایین دست، یکی بدست می آورد:

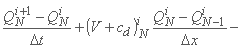
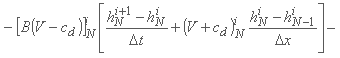
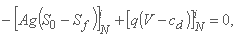
که همراه با یک رابطه به عنوان Q_Nⁱ⁺¹ = f_d(h_Nⁱ⁺¹) حل می شود (برای مثال تابع f_d ممکن است منحنی رتبه بندی این بخش باشد). با شاخص N آخرین نقطه شبکه فضایی مشخص شده است، که در x_N = L قرار دارد.

این طرح بدیهی است که یک خطی است، زیرا همه اصطلاحات معادلات با استفاده از مقادیر شناخته شده در سطح زمان i ارزیابی می شوند (به استثنای متغیرهای جریان ناشناخته Q_jⁱ⁺¹ و h_jⁱ⁺¹ از x_j در سطح زمان فعلی i + 1).