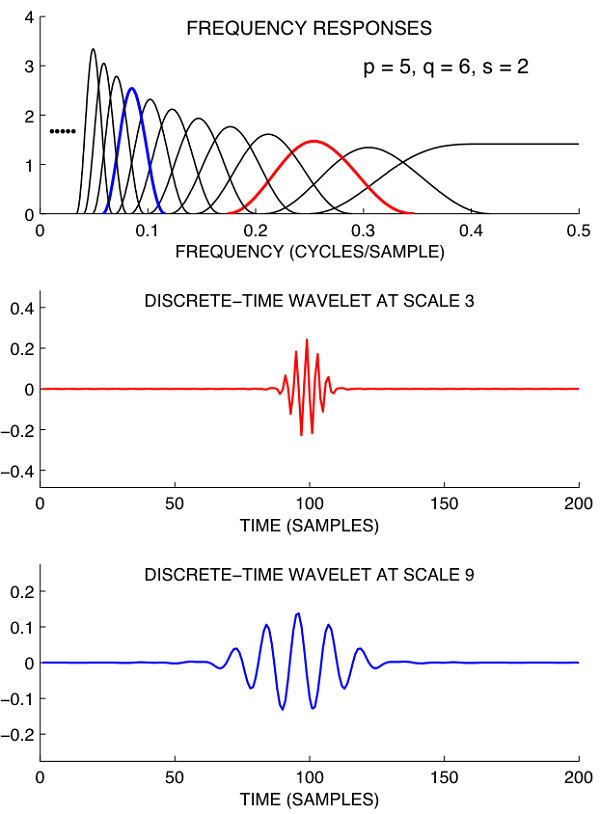
موجک (به انگلیسی: Wavelet) دسته‌ای از توابع ریاضی هستند که برای تجزیه سیگنال پیوسته به مؤلفه‌های فرکانسی آن بکار می‌رود که رزولوشن هر مؤلفه برابر با مقیاس آن است. تبدیل موجک تجزیه یک تابع بر مبنای توابع موجک می‌باشد. موجک‌ها (که به عنوان موجک‌های دختر شناخته می‌شوند) نمونه‌های انتقال یافته و مقیاس شده یک تابع (موجک مادر) با طول متناهی و نوسانی شدیداً میرا هستند.

چکیده

این مقاله بر استخراج ویژگیها از سریهای زمانی و سیگنالها با استفاده از تبدیلات فوریه و موجک متمرکز است. این وظیفه در طبقه بندی سه گروه داده دسته اول (ARR)، دسته دوم (CHF) و دسته سوم (NSR) سری زمانی انجام می شود. رویکرد ما شامل استفاده از مقیاس (به عنوان مثال نمایش 2D ویژگی های استخراج شده 1D) به عنوان ورودی برای آموزش شبکه عصبی (NN) است. ما کارهای مختلف را با استفاده از پایتون به عنوان یک زبان برنامه نویسی انجام دادیم. نتایج ارائه شده در پایان رضایت بخش است و تناسب رویکرد را نشان می دهد.

مقدمه

بسیاری از مشکلات علم داده به عنوان مثال در پیش بینی آب و هوا و غیره با داده هایی همراه است که در طول زمان متفاوت است. ما به همان داده ها به صورت سری زمانی (TS) یا سیگنال اشاره می کنیم. سپس می توانیم همان روش های استخراج را برای TS استفاده کنیم. چه برای طبقه بندی و چه برای کارهای رگرسیون، استخراج ویژگی، گام مهمی است که بر صحت پیش بینی های مورد نظر تأثیر می گذارد.

در این مقاله، ما ابتدا مزایا و معایب استفاده از تبدیل فوریه و موجک ها را در یک مجموعه داده ارائه می دهیم. سپس، توضیح می دهیم که چگونه می توان از نمای 2 بعدی ویژگی های 1 بعدی استخراج شده به عنوان ورودی برای آموزش شبکه عصبی استفاده کرد.

به منظور کسب بینش در مورد داده ها، ما ابتدا با کاوش در مجموعه داده های موجود که شامل داده های جمع آوری شده از بخش های طبقه بندی شده در سه گروه است، شروع می کنیم. همانطور که در شکل 1 نشان داده شده است.

شکل 1: نمایش سه کلاس در داده های ما، در دسته اول آبی (ARR)، در دسته دوم قرمز (CHF) و دسته سوم (NSR) به رنگ سبز.

روش شناسی

در این بخش، ما روش خود را بر اساس تبدیل فوریه (FT) و موجک¹ برای استخراج ویژگی ها به منظور طبقه بندی سیگنال ها در سه کلاس مختلف ارائه می دهیم: دسته اول (ARR)، دسته دوم (CHF) و دسته سوم (NSR)

قبل از این، ما باید بین سیگنال زمان پیوسته و گسسته تفاوت قائل شویم تا یک معادله فوریه گسسته یا پیوسته را اعمال کنیم. اگر سیگنال یک پدیده به طور مداوم اتفاق می افتد، پس می توانیم آن را تابعی از یک متغیر زمان نشان دهیم... بنابراین، 𝑥(𝑡) مقدار سیگنال 𝑥 در زمان t است، دامنه آن زیرمجموعه اعداد واقعی است. ما سپس از یک سیگنال مداوم صحبت می کنیم.

با این حال، برای یک سیگنال زمان گسسته، مقادیر فقط در مراحل زمانی مشخص تعریف می شوند، برای مثال در هر ثانیه تعریف می شود:

t = 1s, t = 2s, t = 3s

در مثال حاضر ما با یک سیگنال مداوم سروکار داریم، بنابراین در ادامه نحوه استفاده از تبدیل فوریه و موجک ها را روی این سیگنال پیوسته نشان می دهیم.

(1) لازم به ذکر است که این دو تکنیک قسمت قابل مشاهده از یک کوه یخ است؛ زیرا پردازش سیگنال یک زمینه گسترده است.

تبدیل فوریه

تجزیه و تحلیل فوریه برای مطالعه تناوب در یک سیگنال توسعه یافته است و ایده اصلی این روش تجزیه سیگنال در اجزای دوره ای آن است. تناوب هنگامی که به سیگنال می رسد یک مفهوم اساسی است، به این معنی که اگر سیگنال حاوی الگویی باشد که پس از یک دوره زمانی خاص تکرار شود، ما آن را سیگنال دوره ای می نامیم. به مدت زمان تکرار یک سیگنال دوره ای، دوره called گفته می شود و معکوس دوره به عنوان فرکانس، named نامگذاری می شود، برای سیگنالی با دوره 1 ثانیه، فرکانس آن 1 واحد است. بنابراین برای یک سیگنال دوره ای تعریف برای تبدیل فوریه مداوم F(k) از توصیف حوزه زمان سیگنالی که به عنوان noted (noted) ذکر شده است با این معادله تعریف می شود:

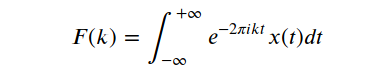
بر اساس فرمول اولر، معادله (1) را می توان با استفاده از توابع سینوس و کسینوس در قالب دیگری نوشت:

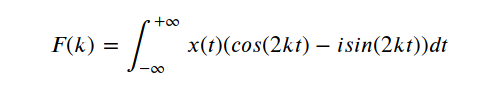
پس از استفاده از تبدیل فوریه بر روی سیگنال، اطلاعات مربوط به فرکانس های مولفه سیگنال، F(k) را در نماد خود بدست خواهیم آورد. در این مرحله ما معمولاً در مورد فضای فرکانس یا توصیف دامنه فرکانس صحبت می کنیم.

هدف از کاربرد تبدیل فوریه تجزیه سیگنال اصلی به مجموع سیگنالهای ساده آن است، مهم نیست که سیگنال اصلی چقدر پیچیده به نظر می رسد. ما به سیگنالهای ساده تر، به عنوان توابع مثلثاتی سینوس و کسینوس اشاره می کنیم. به طور کلی وقتی از سیگنالی در حوزه زمان به دامنه فرکانس حرکت می کنیم، در مورد عکس از تبدیل مستقیم فوریه (FT) صحبت می کنیم تا از فرکانس به زمان دیگر تغییر یابد، معادله تبدیل وارون فوریه نامیده می شود.

برای نشان دادن معادله بعدی با یک مثال، ما از یک مجموعه داده مصنوعی استفاده خواهیم کرد که در آن تعدادی فرکانس منفرد را شامل می شود. در پایتون می توان FT سیگنال را با کتابخانه SciPy محاسبه کرد تا مقادیر فرکانس اجزای سیگنال را بدست آورد.

شکل 2: داده های مصنوعی، در جعبه اول افقی سیگنال کامل را به رنگ سیاه رسم می کنیم، جعبه های بعدی در خطوط قرمز، آبی و سبز به ترتیب مولفه های مربوط به فرکانس های 2، 5 و 3 هستند. در کادر عمودی نتیجه تبدیل فوریه را نشان می دهیم.

در شکل 2 خط سیاه مربوط به سیگنال کامل ساخته شده به عنوان ترکیبی خطی از توابع مثلثاتی است که به ترتیب با خطوط آبی، قرمز و سبز با فرکانس های 2، 5 و 3 رسم شده است. از سیگنال کامل اصلی، این فرکانسها در این مرحله ناشناخته هستند، درست پس از تبدیل فوریه، طیف فرکانسی را می گیریم که سیگنال کامل را تشکیل می دهد، همانطور که در جعبه عمودی با رنگ بنفش ترسیم شده است.

به سمت یک مدل طبقه بندی:

بازگشت به مثال سیگنال مصنوعی که اجازه تجزیه واضح در تبدیل فوریه را می دهد، ما پیشنهاد می کنیم تمام قله های موقعیت های حداکثر را از حوزه فرکانس جمع آوری کنیم، به عنوان مثال با استفاده از قله های کتابخانه scipy، و از آنها به عنوان ویژگی استفاده کنیم.

با این کار، سیگنال دارای برچسب "مصنوعی" دارای یک ردیف از حداکثر موقعیت های مرتبط خواهد بود، در اینجا قله ها به راحتی به صورت زیر شناخته می شوند:

 peak_1: (x_1=2, y_1=4 ), peak_2: (x_2=5 , y_2=1.5 ), peak_3: (x_3=3 , y_3=9 )

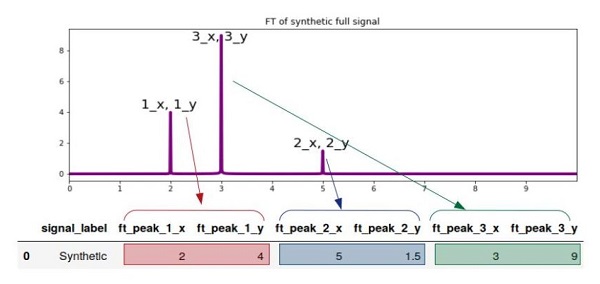
شکل 3: طرح واره نمایانگر تکنیک استخراج ویژگی ها از تبدیل فوریه.

دنبال کردن علامت گذاری در جدول فوق به این معنی است که ویژگی ft_peak_1_x مختصات x اولین فرکانس برای سیگنال است و ویژگی ft_peak_1_y مختصات y است. ویژگی ft_peak_2_x مختصات x فرکانس دوم شناسایی شده و غیره است. سپس ویژگی های ما در مثال سیگنال برچسب خورده "مصنوعی" عبارتند از: ft_peak_1_x، ft_peak_1_y، ft_peak_2_x، ft_peak_2_y، ft_peak_3_x، ft_peak_3_y.

در مواردی که مجموعه سیگنالهای داده ما امکان شناسایی فرکانس مشخص را فراهم می کند، می توانیم یک فریم داده را برای آموزش الگوریتم طبقه بندی تغذیه کنیم.

ما می توانیم با افزودن ویژگی های بیشتر در کاوش سایر تکنیک های پردازش سیگنال را بهبود بخشیم، مانند تراکم طیفی قدرت (PSD) که با اندازه مربع تبدیل فوریه ارائه می شود. حتی بیشتر، می توانیم ویژگی های آماری مانند میانگین، متوسط ​​و واریانس مقادیر را اضافه کنیم. همه اینها به عنوان ستونهای بیشتری در قاب داده ترجمه می شوند.

پس از تبدیل مجموعه داده به یک چارچوب داده قابل بهره برداری، مرحله بعدی انتخاب الگوریتم طبقه بندی کننده برای آموزش است، با این وجود ما با مطالعه تکنیک دیگری که متناسب با داده های ما باشد ادامه خواهیم داد.

 بیایید FT را با یک سیگنال واقعی استخراج شده از مجموعه داده های حاضر امتحان کنیم. در شکل 4 ما به عنوان سیگنال کامل یک نمونه را دنبال می کنیم و به دنبال آن تبدیل فوریه می شود.

شکل 4: داده دسته ARR به عنوان سیگنال کامل در خط سبز، زیر نتیجه FT به رنگ بنفش.

برخلاف مجموعه بسیار مشخص شده فرکانس های بدست آمده با داده های ترکیبی، در شکل 4 FT شفافیت کمتری دارد، ما موفق به شناسایی برخی قله ها شدیم اما در برخی از فواصل آنها واضح نیستند. چرا فوریه قادر به شکستن سیگنال به وضوح نیست؟ برای پاسخ به این مسئله باید به زمان توجه کنیم. در حالت مصنوعی ما یک سیگنال داریم که توسط سه فرکانس تشکیل شده است و این فرکانس ها به موقع ثابت می شوند، فرقی نمی کنند. تبدیل فوریه زمانی کار می کند که تغییری در زمان اتفاق نیفتد، وقتی در حوزه فرکانس هستیم این وابستگی را از دست می دهیم. به نوعی می توانیم تبدیل فوریه را معامله ای بین اطلاعات زمان و اطلاعات فرکانسی بدانیم. با گرفتن یک FT از یک سیگنال زمان، تمام اطلاعات زمان در ازای اطلاعات فرکانس از دست می رود. سیگنال داده های ما پر از فرکانس هایی است که به موقع متفاوت هستند، به همین دلیل است که نمی توانیم آن را به وضوح در حوزه فرکانس حل کنیم.

موجک

در بخش آخر دیدیم که به روشی برای مدیریت سیگنالهایی نیاز داریم که فرکانسهای سازنده آنها با گذشت زمان متفاوت است (به عنوان مثال داده های حاضر). ما به ابزاری نیاز داریم که از وضوح بالایی در حوزه فرکانس و همچنین در حوزه زمان برخوردار باشد، که به ما این امکان را بدهد که بدانیم سیگنال در کدام فرکانس ها نوسان می کند و در چه زمانی این نوسانات رخ می دهد.

تبدیل Wavelet این دو شرط را برآورده می کند. به منظور حل مشکل از دست دادن فهم و درک از حوزه زمانی، تبدیل Wavelet شکل توابع سینوسی و کسینوسی ساده تبدیل فوریه را اصلاح می کند. در یک موج، تابع مادر از نظر زمان محدود است در مقایسه با فوریه که سینوس و کسینوس از (∞+ ,∞-) اجرا می شوند. برخلاف تجزیه فوریه که همیشه از توابع مبنای نمایی (سینوسی و کسینوسی) استفاده می کند (به معادله های بالا مراجعه کنید)، در تجزیه موجک از یک تابع نوسانی محلی-مکانی به عنوان موجک تجزیه و تحلیل یا مادر استفاده می شود، همانطور که در شکل 5 نشان داده شده است.

شکل 5: تابع حقیقی مورلت مادر.

برای یک سیگنال مداوم، 𝑥(𝑡) از یک بعد، موجک تبدیل شده آن به یک فضای 2 بعدی تعریف می شود:

یک عامل مقیاس بودن و یک فاکتور ترجمه در موجک مادر پیوسته استفاده می شود.

ما موجک را با نام موجک مادرش صدا می کنیم، برای مثال shan برای یک تابع نوع Shannon، و با دو پارامتر دیگر a و b، مانند مورد shan1.5-1.0 در جعبه اول شکل 6، که a = 1.5 و b = 1.0. که b پارامتر فرکانس مرکزی است که برای ساخت موجک استفاده می شود و مربوط به دوره به period = s/b است، جایی که s با مقیاس مطابقت دارد، می تواند هر آرایه ای از مقادیر باشد که به ترتیب افزایش می یابد. a، به پارامتر پهنای باند مرتبط است که میزان حساسیت موجک به فرکانسهای اطراف b را انتخاب می کند. برای توابع پیچیده مادر، مثالی را در کادر دوم در شکل 6 نشان می دهیم، جایی که موجک مادر cgau3 نشان دهنده cgau برای عملکرد پیچیده مادر گاوسی است و عدد 3 به ترتیب مشتق تابع موجک مرتبط است.

به طور خلاصه، اگر یک طیف فرکانسی دینامیکی داشته باشیم، به عبارت دیگر اگر سیگنال ما دارای فرکانسهایی باشد که در زمان تغییر می کنند، پس ما به ابزاری با وضوح نه تنها در حوزه فرکانس بلکه در حوزه زمان، Wavelet نیز نیاز داریم. به طور خلاصه، باید بدانیم که تبدیل موجک ابزاری کارآمد برای تجزیه و تحلیل تغییرات کوتاه مدت در مورفولوژی سیگنال است.

قبل از اعمال تغییر شکل موجک بر روی مجموعه داده های حاضر، بگذارید یک دقیقه به شما نشان دهیم چه نوع عملکردهایی را می توانیم به عنوان یک موجک مادر پیدا کنیم. یک تفاوت بزرگ با تبدیل فوریه، جایی که سینوس و کسینوس به عنوان توابع پایه استفاده می شود این است که برای موجک ها خانواده ای از آنها داریم:

‘Haar’, ‘Daubechies’, ‘Symlets’, ‘Coiflets’, ‘Biorthogonal’, ‘Reverse biorthogonal’, ‘Discrete Meyer (FIR Approximation)’, ‘Gaussian’, ‘Mexican hat wavelet’, ‘Morlet wavelet’, ‘Complex Gaussian wavelets’, ‘Shannon wavelets’, ‘Frequency B-Spline wavelets’, ‘Complex Morlet wavelets’.

انتخاب یک عملکرد مادر خاص بستگی زیادی به سیگنال تحت اصلاح دارد، حتی می توانیم عملکرد موجک خود را ایجاد کنیم.

همانطور که انتظار می رود Wavelet Transform دارای دو شکل متفاوت است. تبدیل موجک پیوسته و گسسته شبیه فوریه است.

شکل 6: برخی از اعضای توابع موجک خانواده برای محاسبه تبدیل مورد استفاده قرار می گیرند. ستون اول توابع موجک است، ستون دوم مربوط به توصیف پارامترهای a و b است.

اکنون ما آماده هستیم که در عمل تغییر شکل موجک اعمال شده بر روی یکی از سیگنالهای مجموعه داده موجود خود را ببینیم. برای تجسم بهتر تحول، ما از یک "𝑠𝑐𝑎𝑙e𝑜𝑔𝑟𝑎𝑚" استفاده خواهیم کرد، ابزاری که طیف 2D را برای تبدیل موج پیوسته (CWT) ایجاد و نمایش می دهد. اسکالوگرام مقدار مطلق ضرایب CWT یک سیگنال را می گیرد و آن را رسم می کند.

شکل 7: جعبه بالا مربوط به فاصله کلاس سیگنال داده ها است: ARR، کادر زیر نتایج پس از استفاده از تبدیل Wavelet با موجک Morlet است.

قبل از عمیق شدن در یک موضوع یادگیری ماشین ارزش درک نتیجه مقیاس نمودار را دارد. در محور عمودی ما دوره را تعریف می کنیم (در بالا تعریف شد)، در محور افقی مقیاس را نشان می دهیم، یک رابطه بین مقیاس و دوره با واسطه فرکانس مرکزی وجود دارد، یک پارامتر از موجک انتخاب شده، frequency  = b/s.

می توانیم هر مشخصه افقی را در مقیاس نمودار به عنوان فرکانس سیگنال کل تفسیر کنیم. واقعیت مشاهده نکردن یک خط پیوسته در شکل ما مربوط به این است که فرکانس های ذکر شده از نظر زمانی مداوم نیستند.

یک نکته بسیار مهم در تمرین ما این واقعیت است که می توان مقیاس را به عنوان یک تصویر، یک تصویر را مانند سایر موارد درک کرد و سپس از مدلی مانند NN برای آموزش طبقه بندی استفاده کرد همانطور که در بخش بعدی به شما نشان خواهیم داد.

کاربرد

آموزش طبقه بندی داده ها با استفاده از اسکالوگرام

تفسیر داده های سری زمانی محیطی اغلب دشوار است، در عین حال تفسیر خودکار داده ها برای بسیاری از جنبه های مهندسی و مدیریتی مفید است، به عنوان مثال در نظارت از راه دور، به عنوان یک تصمیم یکپارچه و... . در این بخش ما یک طبقه بندی به عنوان یک روش سریع شناسایی ناهنجاری انجام می دهیم. واقعیت تبدیل سیگنال های داده به مقیاس نگار به ما امکان می دهد تا از یک مدل محاسباتی بصری برای طبقه بندی انواع مختلف ناهنجاری ها در مجموعه داده های خود استفاده کنیم. با توجه به هر تصویری، می توان ترازوی نمودار را در طیف های RGB تجزیه کرد. یک واقعیت مهم که باید توجه داشت این است که هر ردیف یک ضبط داده با نمونه 128 واحد است، این بدان معنی است که ترازوی یک مولفه سیگنال منفرد یک تصویر 127 در 127 پیکسل را تولید می کند.

داده های ما حاوی نوار قلب از سه گروه افراد، ARR، CHF، NSR است، دو مورد اول مربوط به بیماری ها و گروه سوم افراد سالم هستند. برای طبقه بندی این گروه ها، ما پیشنهاد می کنیم که از شبکه عصبی اساسی با استفاده از TensorFlow 2.0 استفاده کنیم، بنابراین در نظر داشته باشیم که تصاویر ما دارای فرمت 127 پیکسل به شکل ورودی ما هستند و به دلیل RGB در 3 فیلتر تجزیه می شوند، بنابراین مدل ما دارای ویژگی های زیر است:

شکل 8: نمایش شماتیک شبکه عصبی مصنوعی کانولوشن ما.

پس از اجرای 10 دوره با استفاده از شیب تصادفی نزولی به عنوان بهینه ساز، و محاسبه ضرر با استفاده از آنتروپی طبقه بندی پراکنده، معیار دقت عملکرد بسیار خوبی را نشان می دهد، همانطور که در شکل 9 نشان داده شده است.

شکل 9: منحنی یادگیری برای 10 دوره، در خطوط آبی و سبز loss و اعتبار سنجی را رسم می کنیم، به رنگ نارنجی و قرمز صحت و اعتبار را رسم می کنیم.

آخرین مرحله برای تلفیق مدل ما کشف یک معیار مناسب تر برای یک مسئله چند کلاسه است، ماتریس سردرگمی، که در شکل 10 نشان داده شده است.

یک ماتریس سردرگمی ایده خوبی از عملکرد یک مدل طبقه بندی به ما می دهد. هر خط مربوط به یک کلاس واقعی / واقعی است، هر ستون مربوط به یک کلاس تخمینی / پیش بینی شده است. ما مقادیر واقعی را با مقادیر پیش بینی شده مقایسه می کنیم، سپس برای مدلهای خوب باید انتظار تعداد زیادی از عناصر در حالت مورب را داشته باشیم، جایی که همه عناصر پیش بینی شده با عناصر واقعی مطابقت دارند. در حالت ما ما ماتریس سردرگمی را عادی کردیم، بنابراین حداکثر مقدار مورد انتظار در حالت مورب 1 است. از شکل 10 می بینیم که مدل ما به خوبی همه این سه کلاس را پیش بینی می کند زیرا تمام مقادیر مورب بسیار نزدیک به 1 است.

پس از تبدیل داده های موجود به اسکالوگرام، ما به یک نتیجه خوب طبقه بندی برای سه گروه از افراد می رسیم.

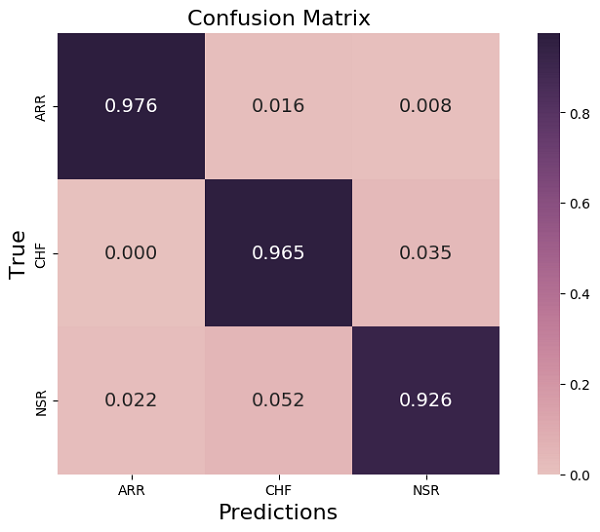
شکل 10: نمودار ماتریس سردرگمی عادی برای نتایج طبقه بندی به دست آمده با CNN قبلاً در شکل 8 تعریف شده است.

نتیجه

در این مقاله دو روش مختلف برای استخراج ویژگی ها از سیگنال ها بر اساس وابستگی به زمان توزیع فرکانس، تبدیل های فوریه و موجک دیده ایم. این توابع سیگنالی را از حوزه زمان به دامنه فرکانس تبدیل می کنند و طیف فرکانس آن را به ما می دهند.

ما یاد گرفته ایم که تبدیل فوریه راحت ترین ابزار استبرای فرکانس های سیگنالی است که در زمان تغییر نمی کنند. با این حال، اگر فرکانس های تشکیل دهنده سیگنال در طول زمان متفاوت باشند، عملکرد عالی عملکرد تبدیل موجک است. آخرین مورد به ما امکان می دهد دامنه فرکانس سیگنال را به عنوان یک تصویر با قالب بندی خروجی به عنوان اسکالوگرام بررسی کنیم و سپس از تکنیک های طبقه بندی تصویر استفاده کنیم.

مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

پروژه تخصصی در لینکدین

×

 براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح