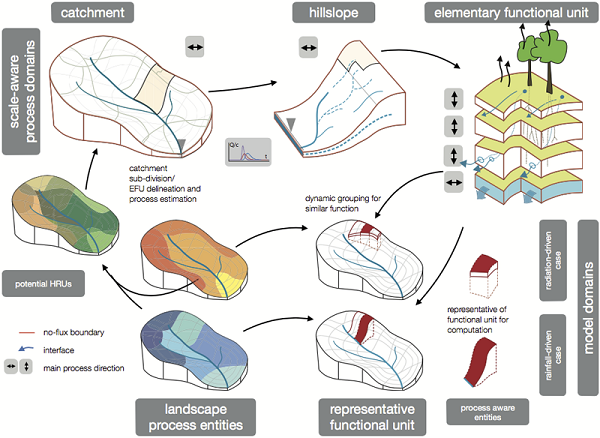
2.8 مدل های کوچک حوضه آبریز

1.2.8. فرمول منطقی

ساده ترین مدل اعمال شده در حوضه های اندازه کوچک به تعیین حداکثر دبی موج سیل با استفاده از فرمول منطقی کاملاً شناخته شده پیشنهاد شده توسط مولوانی (1851) اشاره دارد. طبق این فرمول حداکثر تخلیه Qp (حداکثر) [m3 / s] احتمال بیش از حد p با معادله زیر داده می شود:

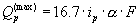
جایی که:

•  i_p شدت توفان باران احتمال بیش از حد پارامتر p است  [mm / min]
•  α ضریب رواناب
•  F منطقه حوضه [km2]
•  16.7 ضریب که از 1000/60 حاصل می شود زیرا شدت باران در [^3-10 متر در 60 ثانیه] و سطح حوضه در [10⁶ متر مربع] بیان می شود.

شدت طوفان باران با توجه به شدت-مدت-فرکانس که به طور مفصل در فصل 2 ارائه شده است محاسبه می شود. فرمول منطقی از مفهوم ایزوکرون ها با توجه به تخلیه Qi در لحظه i با رابطه داده می شود:

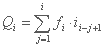
جایی که f_i ناحیه ای است که بین دو منحنی بعدی ایزوکرون تشکیل شده است (به بخش 4 مراجعه کنید).

بیایید یک رویداد طوفان بارانی متشکل از چهار مقدار مجزا  i₁, i₂, i₃, i₄ را در یک بازه زمانی Δt و یک حوضه آبریز که در چهار منطقه ایزوکرون f1،f₁, f₂, f₃, f₄. تقسیم شده است، در نظر بگیریم. حداکثر تخلیه اوج زمانی حاصل می شود که کل منطقه حوضه به تشکیل آن کمک کند و مطابق با رابطه 8.2 تبدیل شود:

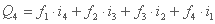
بیایید اکنون در نظر بگیریم که طوفان بارانی از پنج بازه زمانی برابر با Δt تشکیل شده است در حالی که منطقه حوضه هنوز به چهار منطقه فرعی ایزوکرون تقسیم شده است. تخلیه در لحظه i = 5:

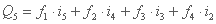
در رابطه f₅i₁ = 0 به عنوان f₅ = 0

اگر در نظر بگیرید که طوفان باران به طور مساوی در زمان توزیع می شود به طوری که i₁ = i₂ = i₃ = i₄ = i or i₁ = i₂ = i₃ = i₄ = i₅ = i, روابط به صورت زیر تبدیل می شوند:

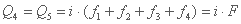
اگر طوفان باران دارای شش، هفت و ... فاصله زمانی از شدت i باشد، حداکثر تخلیه افزایش نخواهد یافت، به عنوان مثال:

=

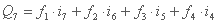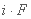
از این رو، اگر طول کل طوفان باران برابر با زمان تاخیر (یا زمان غلظت) τ حوضه آبریز (τ = Δt₁ + Δt₂ + Δt₃ + Δt₄) باشد، حداکثر تخلیه بالقوه حاصل می شود. در نتیجه رابطه اخیر از رابطه اساسی ناشی می شود که ضریب رواناب α برای در نظر گرفتن بارندگی موثر به آن اضافه می شود. به همین دلیل است که رابطه همانطور که از عقلانیت ناشی می شود، فرمول عقلانی نامیده می شود. ذکر خاص این است که فرمول منطقی فقط در حوضه های آبریز با مساحت بیش از 5-10 کیلومتر مربع قابل اجرا است.

با در نظر گرفتن رابطه شدت-مدت-فرکانس نوع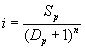 

جایی که S_p و n پارامترهای داده شده روی نقشه ها هستند (به فصل 2 مراجعه کنید). شدت مورد استفاده در فرمول منطقی با جایگزینی مدت زمان طوفان بارانی D_p=τ بدست می آید.

زمان غلظت t_c نشان دهنده زمان حرکت یک ریزش باران است که در انتهای نقطه حوضه تا خروجی آن می افتد. بنابراین، زمان غلظت:

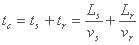
جایی که:

•  t_s زمان انتشار در امتداد شیب
•  t_r زمان انتشار از طول رودخانه
•  L_s طول شیب
•  L_r طول مسیر رودخانه
•  ν_s سرعت آب در امتداد شیب
•  ν_r سرعت آب در امتداد مسیر رودخانه

زمان انتشار در امتداد شیب t_s به طول شیب، به شیب توپوگرافی آن و پوشش زمین بستگی دارد. فرمولهای تجربی بسیاری وجود دارند که مقدار t_s را می دهند. فرمول کربی از جمله آنها است (Mita, 1992):

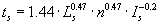
جایی که:

•  n بیانگر "مقاومت" هیدرولیکی زمین در برابر سرریز شدن (به نوعی شبیه ضریب زبری)
•  I_s شیب توپوگرافی از مقدار [مقدار مطلق]
•  t_s زمان انتشار در امتداد شیب [دقیقه]
•  L_s طول شیب [متر]

پارامتر n به عنوان تابعی از پوشش زمین آورده شده است، همانطور که در جدول 1.8 آمده است:

جدول 1.8 مقادیر n از فرمول کربی

Land cover	Corn	Cereal	Green crop	Pasture meadow
n	0.2-0.25	0.4-0.5	0.6	0.8

برخی فرمولهای تجربی دیگر، که مستقیماً مقدار زمان غلظت t_c را می دهند، در زیر آورده شده اند (Musy, 1998):

فرمول ونتورا به طور مستقیم زمان غلظت را نشان می دهد:

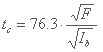
فرمول برانسبی-ویلیامز زمان انتشار را در امتداد شیب می دهد:

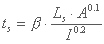
مقررات فنی SNV سوئیس:

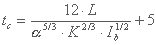
فرمول SCS (خدمات حفاظت از خاک-ایالات متحده آمریکا) زمان کافی را برای شما فراهم می کند:

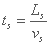
در فرمول های فوق الذکر از علامت های زیر استفاده می شود:

  F منطقه حوضه

  I_b به معنی شیب حوضه آبریز است

  L طول مسیر رودخانه اصلی

  L_s طول از نسخه

  α ضریب رواناب (جدول 2.8)

  K عملکرد پارامتر از مکان و فرکانس طراحی

به مقدار t_s، زمان مسیریابی آب در مسیر اصلی تا خروجی و زمان خیس شدن خاک باید اضافه شود.

جدول 2.8. ضرایب رواناب مطابق مقررات فنی SNV-Switzerland.

Land cover	Runoff coefficient α
Forest	0,1
Prairie, cultivated land	0,2
Vineyard, bare terrain	0,5
Rocks	0,7
Roads without asphalt cover	0,7
Asphalt roads	0,9
Villages, roofs	0,9

سرعت در امتداد شیب ν_s از فرمول SCS به عنوان تابعی از شیب توپوگرافی وانت و ماهیت پوشش زمین در شکل 5.8 آورده شده است:

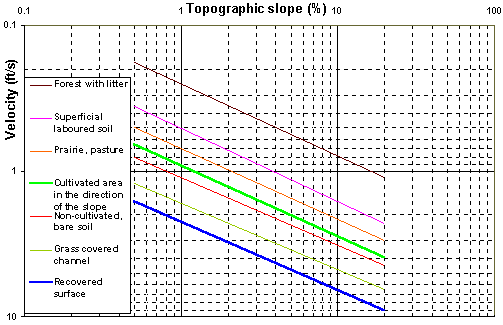
شکل 5.8 سرعتهای سطح در امتداد (US-SCS).

روش دیگر برای ارزیابی زمان سفر در امتداد شیب با استفاده از فرمول تجربی زیر ارائه می شود:

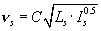
جایی که:

•  L_s [متر]
•  I_s [مقادیر مطلق] 
•  ν_s با واحد [m/s]
•  C ضریب تصحیح در جدول 3.8 آورده شده است

جدول 3.8. مقادیر ضریب تصحیح C.

Land cover	C
Arable terrain ploughed along the slope	0.04
Arable terrain ploughed along the contour lines	0.03
Vineyard	0.024
Orchards	0.022
Pasture	0.20
Meadow	0.016
Forest	0.12

مقادیر تقریبی دیگر سرعتها در امتداد دامنه ها و مسیرهای رودخانه در جدول 4.8 آورده شده است.

جدول 4.8. سرعت جریان در امتداد دامنه ها و مسیرهای رودخانه

Type of the catchment	Velocity along the slope [m/s]	Velocity along the river course [m/s]
Catchments located in the lowland zones	0.05-0.10	0.30-0.50
Catchments located in the high plain zones	0.10-0.15	0.50-1.00
Low hilly catchments	0.15-0.25	1.0-2.5
High hilly catchments	0.25-0.45	2.5-3.5
Mountainous catchments	0.45-0.65	3.5-4.5

برای ارزیابی عملکرد غلظت زمان tc از ویژگیهای مورفولوژیکی حوضه همانطور که در شکل 6.8 نشان داده شده است روابط منطقه ای وجود دارد.

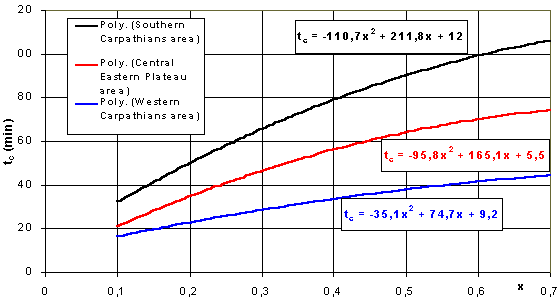
شکل 6.8 عملکرد زمان غلظت ویژگیهای ریخت شناسی حوضه

در شکل 6.8 متغیر x با x=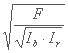 داده شده است

مقادیر زمان سفر در امتداد دامنه ها و مسیرهای رودخانه برای موج سیلاب در اوج در نظر گرفته می شود (احتمالات بیش از حد کم، به عنوان مثال 1٪، 2٪، 5٪).

ضریب رواناب به عنوان تابعی از بافت خاک (سنگین، متوسط ​​و سبک)، ضریب جنگل C_f و دامنه ها بیان می شود. (Mita & Muscanu, 1986):

جدول 5.8. ضریب رواناب به عنوان تابعی از ضریب جنگل نوع خاک و میانگین شیب حوضه.

Light texture
Is	Cf %
	0-20	20-40	40-60	60-80	80-100
5-10	0.44	0.42	0.40	0.38	0.36
10-20	0.46	0.44	0.42	0.40	0.38
20-30	0.48	0.46	0.44	0.42	0.40
30-40	0.50	0.48	0.46	0.44	0.42
40-50	0.52	0.50	0.48	0.46	0.44
Medium texture
Is	Cf %
	0-20	20-40	40-60	60-80	80-100
5-10	0.55	0.53	0.51	0.49	0.47
10-20	0.57	0.55	0.53	0.51	0.49
20-30	0.59	0.57	0.55	0.53	0.51
30-40	0.62	0.60	0.58	0.55	0.53
40-50	0.64	0.62	0.60	0.57	0.55
Heavy texture
Is	Cf %
	0-20	20-40	40-60	60-80	80-100
5-10	0.66	0.63	0.61	0.58	0.56
10-20	0.69	0.66	0.63	0.60	0.57
20-30	0.73	0.69	0.66	0.63	0.60
30-40	0.75	0.72	0.69	0.65	0.63
40-50	0.78	0.75	0.72	0.68	0.65

2.2.8. فرمول کاهش

در مورد حوضه های آبریز که دارای مناطقی بیش از 5-10 کیلومتر مربع باشند، اصل ایزوکرونیسم قابل اجرا نیست زیرا کل منطقه به اوج تشکیل موج سیل کمک نمی کند. از این رو، فرمول منطقی باید به معنای کاهش سطح حوضه با ضریب توان زیر واحد که بین 0.46-0.55 است، اصلاح شود. به عنوان یک قاعده کلی، مقادیر پایین تر برای حوضه های واقع در مناطق کوهستانی قابل استفاده است در حالی که ضرایب قدرت بالاتر برای حوضه های آبریز واقع در مناطق تپه ای و دشت اعمال می شود.

فرمول کلی که برای حوضه های کوچک تا 100-200 کیلومتر مربع اعمال می شود به شرح زیر است:

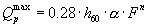
جایی که:

 h₆₀ عمق طوفان باران به مدت یک ساعت با احتمال بیش از حد p

 n = 0.46 - 0.55 ضریب توان است

در فاصله مناطق حوضه ای که بین 10-50 کیلومتر مربع تشکیل شده است، ضریب تصحیح اعمال می شود تا ضریب قدرت از مقدار 1 (همانطور که در فرمول منطقی است) به آرامی به مقادیر فوق الذکر برای حوضه های منطقه حدود 50 کاهش یابد km2

3.2.8. مدل های مبتنی بر فیزیک

با توجه به پیچیدگی آنها، مدلهای ریاضی مبتنی بر معادلات فیزیک ریاضی ممکن است با موفقیت در حوضههای آبریز که در آن یک شبه همگنی خصوصیات فیزیکی (خاک، پوشش زمین) فرض شود، استفاده شود. این فرض ممکن است به طور کلی فقط برای حوضه های کوچک پذیرفته شود و حتی در این موارد تقسیم منطقه حوضه توسط یک شبکه مستطیل شکل اجباری است. از این رو، مدل های مبتنی بر فیزیک (یا مدل های شبه فیزیکی) مدل های توزیعی هستند.

مدل SHE

یکی از مدلهای بسیار شناخته شده از این نوع مدل SHE (Système Hydrologique Européen) است که طی دوره 1978-1982 توسط موسسه هیدرولوژی - والینگفورد (انگلستان)، انستیتوی هیدرولوژی دانمارک (دانمارک) و SOGREAH (فرانسه) تهیه شده است. . این مدل همانطور که در جدول 8.6 نشان داده شده است، فرایندهای زیر را شبیه سازی می کند.

جدول 6.8. فرآیندهای شبیه سازی شده و مدل های مبتنی بر فیزیک.

imulated process	Mathematical Model
Interception	Rutter Model
Evapotranspiration	Penman-Monteith Model
Snowmelt	Energy budget equation / Degree-day method
Overland flow and riverbed flow	Diffusion equation
Water flow in non-saturated zone	Richards equation
Water flow in the saturated zone	Boussinesq equation

یک جز central مرکزی به نام FRAME معرفی داده ها را در مدل سازمان می دهد و عملکرد زیر روال ها را که شبیه سازی فرایندهای مختلف هستند، نظارت و کنترل می کند. این امکان را برای استفاده جداگانه از اجزای مختلف مدل فراهم می کند. اکنون یک روز است که مدل با زیر روال کامل شده است که انتقال رسوبات و مواد محلول را شبیه سازی می کند. این نسخه جدید SHETRAN نام دارد.

نمودار جریان مدل SHE که انتقال اطلاعات بین زیر برنامه های آن را نشان می دهد در شکل 7.8 ارائه شده است. ماژول مبادله با نفوذ و در خط مرزی مبادلات را انجام می دهد.

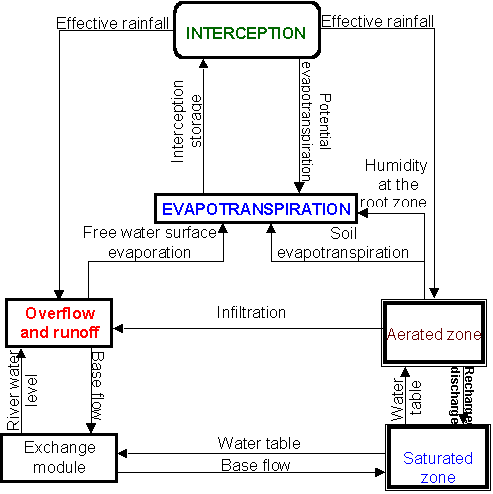
شکل 7.8 انتقال اطلاعات بین ماژول های مدل SHE (Jordan, 1992; Abbot et al., 1986)

TOPMODEL

TOPMODEL (مدل مبتنی بر TOPography) یک مدل شبه فیزیکی است که توسط Bevan و Kirby ساخته شده است. این مدل حول دو ایده اساسی شکل گرفته است، یعنی: رواناب بر روی مناطق کمک کننده متغیر از یک طرف تولید می شود و توپوگرافی بر نحوه تولید رواناب تأثیر می گذارد. TOPMODEL یک متغیر هیدرولوژیکی جدید، یعنی شاخص توپوگرافی، ایجاد می کند که یک تخمین مستقیم از رواناب در حوضه را تشکیل می دهد و بیانگر توانایی اشباع یک نقطه از حوضه آبریز است. به منظور تعیین مقدار شاخص، یک مدل زمینی عددی حاصل می شود. هنگام ایجاد شاخص توپوگرافی، فرضیه زیر در نظر گرفته می شود:

• کاهش نمایی رسانایی هیدرولیکی در اشباع با عمق.
• وابستگی به هدایت هیدرولیکی در حالت اشباع به عمق.
• منطقه غیر اشباع به عنوان یک مخزن جاذبه ساده در نظر گرفته می شود.
• منطقه غیر اشباع بر جریان های جانبی تأثیر نمی گذارد.
• طی یک بازه زمانی رژیم یک رژیم ثابت است.
• شیب منطقه اشباع برابر با سطح خاک است.

با توجه به این مفروضات، شاخص توپوگرافی IT (i) از پیکسل i به این صورت بیان می شود:

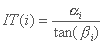
جایی که:

•  α_i منطقه که در پیکسل i تخلیه می شود
•  tan(β_i) شیب سطح

نمودار جریان TOPMODEL در شکل 8.8 ارائه شده است.

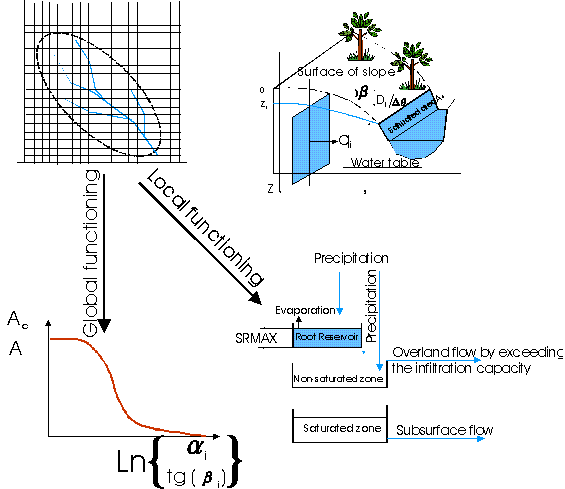
شکل 8.8 طرح TOPMODEL منبع  (Musy، 1998)

مدل موج حرکتی

مدل موج حرکتی روند جریان زمینی را در امتداد یک صفحه شیبدار شبیه سازی می کند که ممکن است عنصری از واحد عرض یک بستر رودخانه یا یک حوضه بزرگ حوضه آبریز باشد. در حالت آخر مساحت حوضه به چندین صفحه تقسیم می شود. رواناب ابتدا در حاشیه انتهای صفحه بالادست یکپارچه می شود و سپس ادغام جدیدی از جریان زمینی در امتداد صفحه دیگر انجام می شود و به هواپیمای قبلی اضافه می شود. روش ادغام طبق خروجی حوضه مطابق با طرحی مبتنی بر طبقه بندی زیرحوضه ای که دستور مداخله در آن تعیین می شود، ادامه می یابد. از این رو، زیرحوضه های مرتبه اول به یک زیرمحدوده سفارش 2 و مرتبه 2 زیر زیرمجموعه ها به دسته فرعی 3 مرتبه و غیره می روند. خروجی صفحه قدامی برای ادغام بعدی به شرط مرزی تبدیل می شود. طرحی از یک مدل موج حرکتی در شکل 9.8 ارائه شده است.

مطابق شکل 9.8 معادله پیوستگی به صورت زیر نوشته شده است:

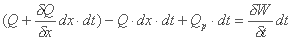
جایی که:

 Q جریان آب در ورودی در عنصر dx

 W حجم ذخیره شده در سطح اولیه dx

 dt فاصله زمانی

 Q_p سهم بارشی موثر p(t) در تشکیل سیل بیش از عنصری از صفحه با پهنای برابر 1.

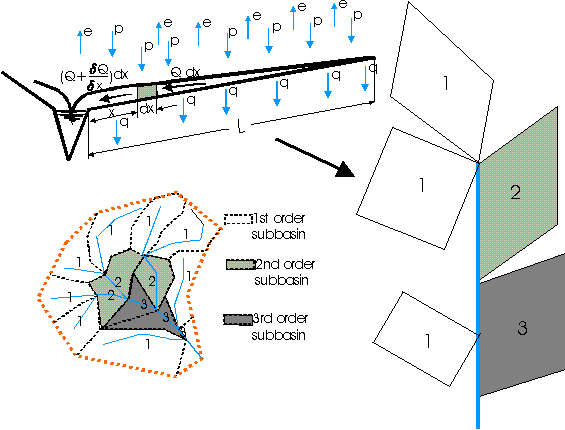
شکل 9.8 طرح مدل موج حرکتی

تغییر حجم معادله نوشته شده است:

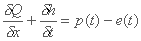
جریان آب ممکن است نوشته شود:

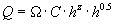
جایی که:

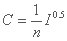
(I شیب صفحه است، n مقاومت هیدرولیکی یا ضریب زبری است).

z = 0.5 زیرا جریان مشابه جریان در محیط متخلخل است

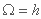 or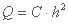 

سرانجام می توان نوشت:

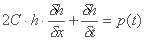
هنگامی که بارندگی h(t) = 0 متوقف می شود و تلفات حاصل از نفوذ q(t)- می شود، سپس:

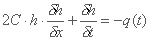
در طول دوره تشکیل سیل، از تبخیر و تعرق غفلت می شود، در غیر این صورت باید از مقدار p(t) کم شده یا به q(t) اضافه شود.

حل معادلات به راحتی با استفاده از روش مشخصه ها یا با یکی از روشهای اختلاف محدود بدست می آید.

تعیین ضریب زبری برای چندین نوع پوشش زمین دشوار است. با استفاده از ایزوتوپ ها برای ارزیابی سرعت در امتداد یک سطح پوشیده شده از مراتع و داشتن شیب 13٪، استانسکو (1973) مقدار n = 0.130 را تعیین کرد.

مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

×

 براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح