کالیبراسیون پارامترها به عنوان شناسایی، ارزیابی، ارزیابی یا برآورد نیز شناخته می شود. در مدل های ریاضی یک سری پارامترها اتفاق می افتد، هر یک از آنها منعکس کننده تأثیر یک یا چند عنصر است که بر پدیده یا روند تحلیل شده عمل می کنند. اگر پارامترها معنای فیزیکی مستقیم نداشته باشند یا قابل اندازه گیری نباشند، تنها راه شناسایی تعیین آنها با روش های ریاضی است.

1.11 روشهای تحلیلی برای محاسبه بهینه پارامترها

این روشها براساس اصول حساب دیفرانسیل است. برای تابعی از یک متغیر، نقطه ثابت *x با محو مشتق اول و حل معادله حاصل تعیین می شود:

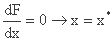
برای تعیین کیفیت نقطه ثابت، که می تواند یک کمینه کننده، یک حداکثر کننده یا یک نقطه خم باشد، ما باید مشتقات مرتبه برتر را ارزیابی کنیم.

اگر اولین مشتق غیر صفر در x* = x، دارای نظم بیشتر از 1، از نظم یکنواخت باشد، *x مربوط به حداقل محلی است اگر مقدار این مشتق مثبت باشد، به ترتیب با حداکثر محلی اگر مقدار باشد منفی. با این حال، اگر اولین مشتق غیر صفر در x* = x، که ترتیب آن بیشتر از 1 است، از یک نظم عجیب و غریب باشد، *x نقطه عطف است.

در مورد تابعی از چندین متغیر F(x) = F(x₁, x₂, ..., x_n) شرط تعیین نقطه ثابت *x این است که هر مشتق جزئی در آنجا از بین برود:

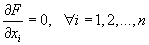
با حل سیستم معادلات به دست آمده، به ناشناخته های *x₁*, x₂*, ..., x_n، مختصات نقطه ثابت *x پی خواهیم برد.

به منظور تعیین نوع نقطه ثابت (حداکثر کننده، کوچک کننده یا نقطه عطف) می توانیم از ماتریس مشتقات جزئی دوم (ماتریس هسی f(x)) استفاده کنیم. روش کلاسیک نیاز به محاسبه هر یک از عوامل تعیین کننده درجه دوم hessian دارد.

در بیشتر موارد، استفاده از یک روش تجربی، با ارزیابی عملکرد f (X) در *x  و پس از آن در چندین نقطه در محله نزدیک *x ، عملی تر است. گسترده ترین روشهای تحلیلی مورد استفاده برای بدست آوردن پارامترهای بهینه عبارتند از: روش حداقل مربعات و روش ضریب لاگرانژ. اگرچه روش لحظه ها از مشتقات استفاده نمی کند، اما در گروه روش های تحلیلی قرار گرفت.

1.1.11 روش حداقل مربعات 

این یک روش بسیار گسترده است که برای تعیین ضرایب معادله رگرسیون استفاده می شود.

1.1.1.11. توابع خطی

بگذارید ابتدا موردی را بررسی کنیم که رابطه آماری بین متغیر توضیح داده شده و توضیحی خطی باشد:

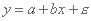دو اصطلاح اول نمایانگر مولفه قطعی (روند) است و عبارت آخر مولفه تصادفی را نشان می دهد (تأثیر عناصر دیگر، علاوه بر x).

با غفلت از اصطلاح تصادفی، پارامترهای a، b خط رگرسیون را که متناسب با داده های داده شده است، تخمین می زنیم. بنابراین یک تابع خطا بدست می آوریم که می تواند به روشهای مختلف تعریف شود:

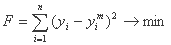
یا

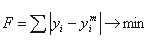
نقاط (x_i, y_i) روی خط رگرسیون است که به عنوان مقادیر نظری در نظر گرفته می شود، در حالی که (x_i, y_i^m) با اندازه گیری بدست می آید (شکل 1.11).

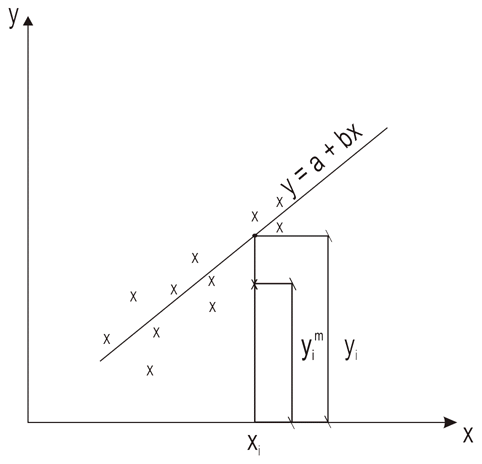
شکل 1.11 اصل حداقل مربعات.

ما میتوانیم بنویسیم:

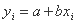
با دانستن اینکه برای شناسایی بهترین پارامترها باید مشتقات تابع F را ارزیابی کنیم، اولین عبارت آن ترجیح داده می شود. بنابراین باید مجموع انحراف مربع ها را بین مقادیر اندازه گیری شده و مقادیر نظری قرار داده شده روی خط رگرسیون به حداقل برسانیم. به همین دلیل است که این فرآیند به عنوان روش حداقل مربعات شناخته می شود.

جایگزینی مقدار y_i در تابع هدف به شرح زیر است:

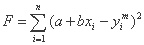
با محو شدن مشتقات جزئی y_i، تابع F به یک سیستم از دو معادله خطی با دو ناشناخته تبدیل می شود که به راحتی حل می شود.

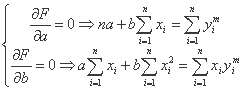
نقطه x* = (a*,b*) با حداقل تابع خطا مطابقت دارد.

همبستگی خطی اغلب در هیدرولوژی مشاهده می شود. به عنوان مثال، رابطه بین حجم سیل و حداکثر جریان از این نوع است. وابستگی بین جریان در دو بخش از رودخانه نیز خطی است.

در شرایط دیگر، متغیر y (x) دارای یک جمله چند جمله ای درجه اول است، اما با استفاده از متغیرهای بیشتر x₁, x₂, ..., x_n (مورد همبستگی خطی چندگانه):

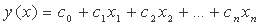
در این حالت تابع هدف به شکل زیر است:

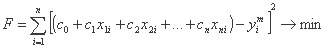
این شرط که هر مشتق جزئی ∂F/∂c₀, ∂F/∂c₁,..., ∂F/∂c_n از بین برود، سیستم خطی Ax = B را به وجود می آورد، جایی که A ماتریس مربع است. بنابراین می توانیم ماتریس معکوس A^-1 را محاسبه کنیم، و محلول x* = (c₁*, c₂*, ..., c_n*)^T با رابطه x = A^-1B داده می شود.

در هیدرولوژی می توان نمونه ای از همبستگی چند خطی را در نظر گرفت (Drobot، 1983): مدل کلاسیک Muskingum برای انتشار امواج سیل:

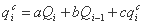
جایی که:

•  q_i^c جریانهای محاسبه شده در انتهای پایین دست بخش رودخانه را نشان می دهد
•  Q_i جریان های بالادستی را اندازه گیری کرد (جریان های پایین دستی اندازه گیری شده با q_i^m نشان داده می شوند)

پارامترهای a، b و c مدل فوق پارامترهایی هستند که عملکرد را به حداقل می رسانند

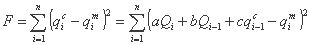
با در نظر گرفتن q_i-1^c ≈ q_i-1^m (Drobot، 1983)، عملکرد به شرح زیر است:

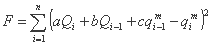
پس از آن مشتقات جزئی ∂F/∂a, ∂F/∂b, ∂F/∂c را محاسبه می کنیم و سیستم معادلات را حل می کنیم، بنابراین پارامترهای a، b و c معادله انتشار را بدست می آوریم.

در مورد منحنی درجه بندی یا منحنی تخلیه، که با یک تابع سهموی بیان می شود، از همان روش حداقل مربعات استفاده می شود:

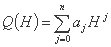
پارامترها با حل سیستم زیر از معادلات خطی (با توجه به ناشناخته های ai) تعیین می شوند:

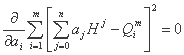
باید بگوییم، اگرچه در بیان منحنی تخلیه ارتفاع H دارای شاخص های مختلف است: H⁰, H¹, H²,..., اما رابطه با توجه به پارامترهای a₀, a₁, a₂,... هنوز خطی است. به همین دلیل است که سیستم معادلات بدست آمده از بین رفتن مشتقات نیز خطی است.

مثال دیگر استفاده از روش حداقل مربع، تعیین مختصات هیدروگراف واحد است. در این حالت، تابع هدف را می توان به شکل زیر بیان کرد:

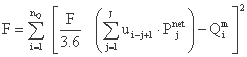
جایی که:

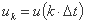•   نشانگر مختصات هیدروگراف واحد است
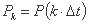•   بارش بین لحظات Δt(k-1) و kΔt افتاده است

جریان های تخمینی با توجه به u_k (واحد هیدروگراف واحد) خطی هستند. محو شدن مشتقات منجر به سیستمی از معادلات خطی می شود. با حل آن می توان مقادیر u_k را شناسایی کرد.

2.1.1.11. توابع غیر خطی در پارامترها

در بسیاری از موارد مدل ریاضی وابستگی بین متغیرهای y و x از نوع غیرخطی است. از تکنیک حداقل مربعات نیز می توان استفاده کرد، اما سیستم حاصل از معادلات غیرخطی است و در نتیجه حل آن دشوار است. یک راه حل این است که بیان غیر خطی را با استفاده از عملگرهای مختلف خطی کنید: لگاریتم ها، ریشه مربع یا سایر تحولات ریاضی.

خطی سازی توابع غیرخطی

یک روش معمول برای غلبه بر این دشواری استفاده از یک تغییر متغیر است مانند: با عبور از سیستم اصلی مختصات (x، y) به سیستم جدید (X، Y)، یک وابستگی خطی بین متغیرهای تبدیل شده Y_i^m, X_i بدست می آوریم.

بیایید به عنوان مثال منحنی نفوذ Horton را در نظر بگیریم. شدت نفوذ شناخته شده است به عبارت:

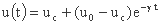
جایی که:

•  u(t) میزان نفوذ در لحظه t، بیان شده در mm/min ؛
•  u₀ نرخ نفوذ در دقیقه اول (mm/min) ؛
•  u_c نرخ نفوذ پس از تثبیت فرآیند (mm/min) ؛
•  γ یک پارامتر (در min^-1 یا hours^-1 بیان می شود).

از آنجا که فرمول هورتون با توجه به پارامتر γ غیرخطی است، ما باید معادله نفوذ را خطی کنیم. بنابراین، ما باید معادله را به شکل زیر بنویسیم:

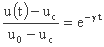
با استفاده از لگاریتم بدست می آوریم:

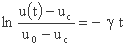
نقاط اولیه (t_i,u_i) در سیستم مختصات (t، u) در سیستم (X، Y) تبدیل می شوند (X_i,Y_i) ؛ تحولات استفاده شده عبارتند از:

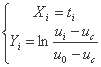
جایی که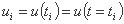 

در سیستم مختصات (X، Y) منحنی Horton به خط مستقیم Y = AX تبدیل می شود (شکل 2.11)، جایی که:

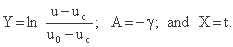
شیب این خط مستقیم  Y/X = -γ؛ بلافاصله نتیجه می شود که A = -γ.

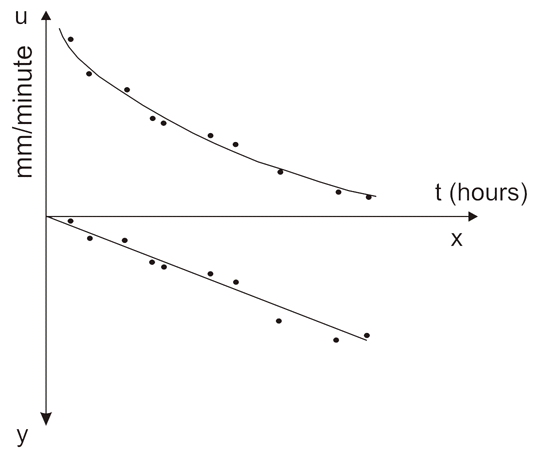
شکل 2.11 ارزیابی پارامتر γ منحنی نفوذ هورتون.

از آنجا که Y = AX داریم، می توانیم Y_i = AX_i بنویسیم. تابع هدف:

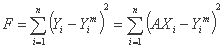
برای ارزیابی A باید مشتق تابع هدف را محاسبه کنیم. نتیجه می شود که

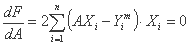
ما برای A بدست می آوریم:

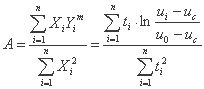
خط بندی همیشه آسان نیست.

حال مورد منحنی تخلیه را که به شکل سهموی بیان شده است بررسی می کنیم:

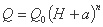
که در آن Q₀, a, n پارامترهایی هستند که باید پیدا شوند.

رابطه فوق پس از اعمال لگاریتم ایجاد می شود:

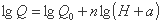
رابطه فقط خطی است اگر مقدار مناسبی برای پارامتر a در نظر بگیریم. از آنجا که a ناشناخته است، ما باید چندین تلاش پی در پی را با اختصاص مقادیر مختلف به آن انجام دهیم تا زمانی که داده های تجربی شرایط خطی را برآورده کنند (شکل 3.11). پارامتر a که منجر به تقسیم تقریباً مستقیم مقادیر اندازه گیری شده می شود به عنوان محتمل ترین مقدار حفظ می شود.

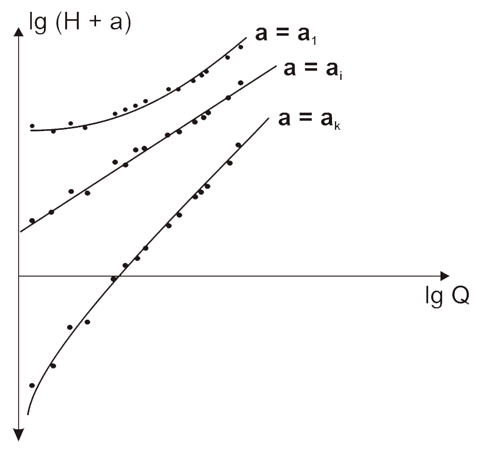
شکل 11.3 ایجاد مقدار پارامتر a.

پس از یافتن پارامتر a، باید پارامترهای خط رگرسیون را در سیستم مختصات (X، Y) تعیین کنیم، جایی که:

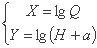
معادله خط مستقیم:

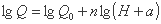
می توان به صورت زیر نوشت:

X = A + BY

جایی که A = lg Q₀ و B = n.

ما ابتدا پارامترهای A، B خط رگرسیون را در سیستم تعیین می کنیم (X، Y) و پس از آن از تبدیلات معکوس استفاده می کنیم: Q₀ = 10^A و n = B، که ما را به مقادیر Q₀ و n می رساند.

رویکردهای عددی در مورد توابع غیرخطی

اگر تابع تقریب با استفاده از روشهای تحلیلی کلاسیک (از بین رفتن مشتقات جزئی) از نظر پارامترها غیرخطی باشد، ما باید یک سیستم از معادلات غیر خطی بدست آوریم.

در حالت خاصی که تعداد مجهولات برابر با یک باشد، باید یک معادله غیرخطی واحد را حل کنیم. در این حالت از روش مماس اغلب استفاده می شود.

بیایید فرض کنیم که تابع غیر خطی f (x) پس از تمایز تابع هدف F (x) بدست آمده دارای یک ریشه α در فاصله [a، b] باشد. α در حقیقت نقطه ای را نشان می دهد که منحنی f(x) محور Ox را قطع می کند. علاوه بر این، ما این فرض را می گیریم که f(x) یک تابع دو برابر به طور مداوم قابل تغییر است و مشتق آن علامت [a، b] را تغییر نمی دهد.

بگذارید x₀ اولین تقریب α باشد. ما با x_i نقطه ای را نشان می دهیم که خط مماس نمودار f(x) در (x₀, f(x₀)) محور x را قطع می کند. توجه کنید که xi تقریب بهتری برای α است. این فرایند با در نظر گرفتن x2، رهگیری x خط مماس در (x₁, f(x₁)) و غیره ادامه می یابد (شکل 11.4).

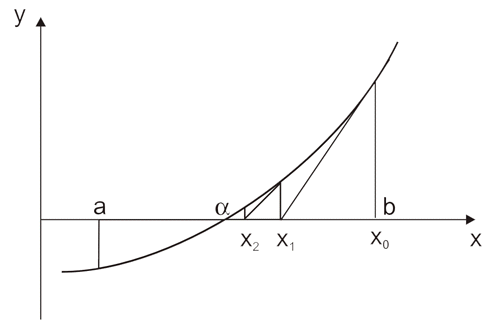
شکل 4.11. تصویر گرافیکی روش مماس.

به طور کلی، معادله خط مماس در نقطه (x_k, f(x_k)) است:

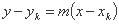
که در آن m شیب خط مماس به نمودار f(x) در نقطه (x_k, f(x_k)) است ؛ اما شیب در این نقطه (x_k, f(x_k)) فقط f'(x) است و معادله مماس را می توان به صورت زیر نوشت:

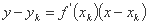
بگذارید x_k+1 نقطه ای را نشان دهد که خط مماس با محور Ox قطع می شود. در این مرحله y = 0, x = x_k-1 داریم و بدست می آوریم:

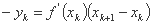
از آنجا که y_k= f(x_k)، نتیجه آن است

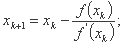 k = 0,1,2,…

این فرمول عود با تکرارهای پی در پی توالی x₀, x₁, x₂,... را تولید می کند که به α جمع می شود.

درصورتی که تابع هدف F تابعی متغیر از n-متغیرهای x₀, x₁, x₂,... باشد، محو شدن مشتقات جزئی ما را به سمت یک سیستم معادلات هدایت می کند:

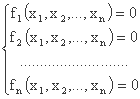
اگر این سیستم غیرخطی باشد، اغلب از روش نیوتن-رافسون استفاده می شود، که روش مماس را به حالت n بعدی گسترش می دهد. توالی تکرارهای پی در پی با فرمول تکرار زیر تعریف می شود:

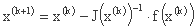
جایی که:

 x^(k) نقطه مختصات (x₁^(k), x₂^(k), ..., x_n^(k) ) در تکرار k-th است.

 f(x^(k)) بردار است (f₁(x^(k)), f₂(x^(k)), ..., f_n(x^(k)))^T

 J(x^(k))^-1 معکوس ماتریس یعقوبی است (ماتریس مشتقات جزئی f₁, f₂, ..., f_n توابع در نقطه x = x^(k):

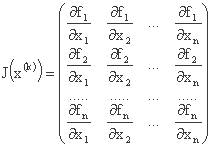
تکرارها تا زمانی که اجزای بردار f(x^(k))بسیار نزدیک به صفر باشد، یا به طور معادل، تا زمانی که شرط زیر برآورده شود ادامه می یابد:

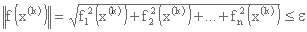
که بدان معنی است که هنجار (یا اندازه) بردار f(x) تحت یک مقدار مشخص، ε، به اندازه کافی نزدیک به صفر کاهش می یابد.

بیایید به عنوان مثال معادله منحنی تخلیه را که در فرم نوشته شده است، در نظر بگیریم

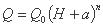
تابع هدف در این مورد است:

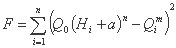
بردار مشتقات جزئی F (نشان داده شده توسط 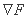) دارای عبارت زیر است:

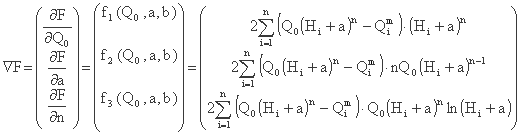
ماتریس یعقوبی را می توان به ترتیب محاسبه کرد.

با این حال عبارت حاصل از آن پیچیده است. به همین دلیل، به طور کارآمد تر می توان بیان منحنی رتبه بندی را خطی کرد.

2.1.11. روش ضرب لاگرانژ

بسیاری از مشکلات بهینه سازی شامل به حداکثر رساندن یا به حداقل رساندن تابعی از چندین متغیر (x₀, x₁, x₂,..., x_n) تحت یک یا چند محدودیت است که می تواند برابر یا نابرابری باشد.

با توجه به اینکه ناشناخته ها مختصات یک نقطه x را در فضای n بعدی نشان می دهند، می توان یک مسئله بهینه سازی را به شکل زیر بیان کرد:

مقدار F(x), 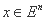 را بهینه کنید، منوط به h_j(x) = 0, j = 1, 2, ..., m.

توجه داشته باشید که محدودیت های نابرابری را می توان به برابری تبدیل کرد. به عنوان مثال، محدودیت های دامنه متغیرها x_min,i ≤ x_i ≤ x_max,i , i = 1, 2, ..., n  را می توان به صورت زیر نوشت:

g(x_i) = x_i - x_min,i ≤ 0، و به ترتیب:

g(x_i) = x_i - x_max,i ≤ 0

هر محدودیت g_j(x) ≥ 0 را می توان در یک محدودیت برابری با معرفی یک متغیر ساختاری ν_j تغییر داد:

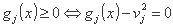
محدودیت های نوع "≤ 0" با ضرب ساده با -1 به شکل "≥ 0" کاهش می یابد. به جلو آنها با استفاده از متغیرهای ساختگی در برابری تبدیل می شوند.

بنابراین هر محدودیتی را می توان به عنوان محدودیت برابری نوشت.

ثابت شده است که مشکل:

بهینه سازی F(x₁, x₂,..., x_n)

مشمول محدودیت های:

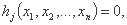 j = 1,2,....,m; m<n

با یافتن نقاط ساکن تابع لاگرانژ برابر است:

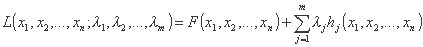
پارامترهای λ_j علاوه بر این به عنوان ضرایب لاگرانژ شناخته می شوند.

به جلو، با محو شدن مشتقات تابع لاگرانژ، می توانیم نقاط ساکن تابع L را پیدا کنیم:

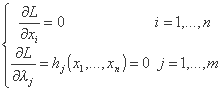
بیایید مدل کلاسیک Muskingum را در نظر بگیریم که در آن مجموع ضرایب a، b، c برابر با واحد است:

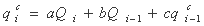
با شرط a + b + c = 1

تابع هدف مورد استفاده برای شناسایی پارامترهای a، b، c را می توان به صورت زیر نوشت:

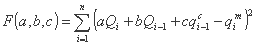
با محدودیت: φ = a + b + c -1 = 0.

ما از نت های فعلی استفاده می کنیم: q_i^c و q_i^m به ترتیب محاسبه می شوند، جریان پایین دست اندازه گیری شده در لحظه i است، در حالی که Q_i جریان بالادست در همان لحظه است. ما باید  q_i-1^c ≈ q_i-1^m تقریبی داشته باشیم.

به جلو، ما تابع لاگرانژ را خواهیم ساخت (Drobot، 1984):

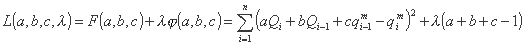
و تنظیم کنید که مشتقات جزئی آن ناپدید شوند:

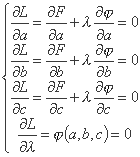
با حل این سیستم ضرب γ و مقادیر a، b، c بدست می آوریم که ما را به حداقل تابع F می رساند.

در این حالت می توان سیستم را نوشت (Drobot، 1984):

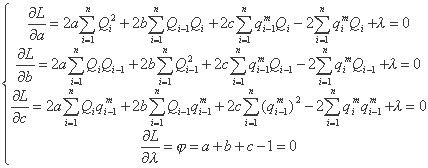
حل این سیستم 4 معادله خطی با 4 مجهول به هیچ وجه کار سختی نیست.

3.1.11. روش لحظه ها

یکی از تکنیک هایی که برای شناسایی پارامترهای هیدروگراف واحد استفاده می شود، روش لحظه ها است (Nash, 1960).

هیدروگراف واحد معمولاً توسط یک تابع گاما با 2 پارامتر تعریف می شود. بنابراین برای تعیین پارامترها به دو معادله نیاز داریم. برای این منظور ما باید دو لحظه اول را با توجه به مبدا، هر دو واحد هیدروگراف و میزان بارش خالص محاسبه کنیم.

تابع گاما با دو پارامتر عبارت زیر را دارد:

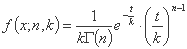
و لحظات سفارش اول و دوم عبارتند از:

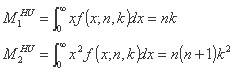
می توان ثابت کرد، با در نظر گرفتن این که مقدار جریان به صورت کانولوشن بارش خالص و هیدروگراف واحد بدست می آید، برابری های زیر برقرار است:

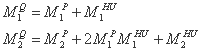
که در آن شاخص پایین تر ترتیب لحظه (1 یا 2) را نشان می دهد و شاخص برتر به جریان (Q)، بارش خالص (P) و واحد هیدروگراف (HU) اشاره دارد.

با جایگزینی عبارات M₁^HU و M₂^HU در دو معادله، فرمولهای زیر را برای k و n بدست می آوریم.

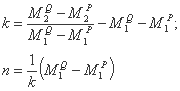
مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

پروژه تخصصی در لینکدین

×

 براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح