3.10 خطاهای تحقیق و اندازه گیری

چندین نوع خطا وجود دارد که می تواند رخ دهد. در اولین بازرسی، برخی از اینها ممکن است به یک باره شناسایی و اصلاح شوند، برخی از آنها یادداشت و علامت گذاری شده و برخی دیگر ممکن است شناسایی نشوند. آن ها هستند:

1. "درجا":

• اشتباه خواندن، اعشار دهی بی جا، خطاهای کپی برداری و اشتباهات حساب.
• قرائت انباشته در طی چندین روز به صورت یک روزه وارد شده است.
• قرائت صحیح که در روزهای اشتباه، مداوم یا فقط گاهی انجام می شود.
• حذف سهوی مشاهدات انجام شده اما ذکر نشده است.
• خطاهای گاه به گاه به دلیل اختلال موقتی گیج یا قرار گرفتن در معرض آن.
• خطاهای سیستماتیک ناشی از تغییر تدریجی قرار گرفتن در معرض در طی یک دوره طولانی (سالها) یا یک نشت سنج با افزایش تلفات.

2. تحقیقات آماری بر اساس فرضیه های خاص. فرضیه های تجزیه و تحلیل آماری:

• اندازه گیری ها مقادیر واقعی را منعکس می کنند - این فرضیه در عمل استفاده نمی شود.
• سازگاری داده ها - هیچ تغییری در شرایط داخلی سیستم در طول دوره مشاهده وجود ندارد.
• سری داده ها ثابت هستند - خصوصیات قانون آماری به مرور تغییر نمی کنند.
• داده ها همگن هستند - یک سری داده ها همگن در نظر گرفته می شوند:
• این دو یا چندین رویداد مختلف را منعکس می کند (به عنوان مثال رژیم جریان پایین دست تلاقی دو زیرحوضه با رفتارهای مختلف هیدرولوژیکی)
• این رویداد غیر ثابت است (به عنوان مثال تغییرات آب و هوایی، تغییر رژیم جریان)
• سری داده ها تصادفی و ساده است. اگر همه مشاهدات از یک جمعیت تشکیل شده و مستقل از یکدیگر باشند، مجموعه تصادفی و ساده است.
• سری باید به اندازه کافی طولانی باشد - طول یک سری بر روی خطاهای نمونه تأثیر می گذارد.

آزمونهای آماری

دسته های زیر از آزمون های آماری هستند:

1. تست های متعاقب خصوصیات ریاضی آنها. در بیشتر موارد، این آزمونها بر اساس قانون عادی است و وجود یک متغیر تصادفی مرجع X را فرض می کند. س isال این است که آیا اگر X نرمال نباشد نتایج معتبر هستند: اگر نتایج معتبر باشند، آزمون "قوی" است. این بدان معناست که آزمون نسبت به برخی اصلاحات مدل تقریباً حساس نیست.

2. آزمون های بعدی شی آنها در چهار دسته طبقه بندی می شوند:

• آزمونهای همگنی یا آزمایشات مقایسه نمونه ها

اگر دو نمونه داده شود، از اندازه n₁ و n₂، آیا می توان پذیرفت که این نمونه ها بخشی از یک جمعیت بودند، اما بین آنها مستقل بودند؟

از نظر ریاضی، مسئله را می توان به صورت زیر بیان کرد: می توان آن را در اولین نمونه تحقق یک متغیر تصادفی X₁ و تابع تقسیم مجدد (F₁(x و در نمونه دوم تحقق یک متغیر تصادفی X₂ و تابع تجزیه مشاهده کرد. (F₂(x

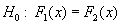
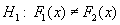
• قابل آزمایش است:

مقایسه مقادیر مشخصه نمونه با مقدار مرجع به معنای تأیید این است که آیا می توان مشخصه را برابر با مقدار مرجع پذیرفت. به عنوان مثال H₀: μ = μ₀ که μ₀ مقدار مرجع است و μ مقدار ناشناخته است.

• آزمون انطباق

مقایسه مقادیر مشخصه نمونه با مقدار مرجع به معنای تأیید این است که آیا می توان مشخصه را برابر با مقدار مرجع پذیرفت. به عنوان مثال H₀: μ = μ₀ که μ₀ مقدار مرجع است و μ مقدار ناشناخته است.

• آزمون تنظیم

تأیید می کند که آیا یک نمونه داده شده بخشی از یک جمعیت خاص است.

• آزمون خود همبستگی

تأیید می کند آیا پیوندی بین داده های تقویمی یک سری مشاهده وجود دارد یا خیر. اندرسون توزیع ضریب همبستگی را برای یک جمعیت عادی مطالعه کرده است. در این حالت، ضریب همبستگی خودکار را می توان برای جفت مقادیر (x₁, x₂), (x₂, x₃), …, (x_n-1, x_n), و (x_n, x₁) محاسبه کرد. برای سری n، اندرسون مقادیر را در 75 محدود کرد. ضریب همبستگی، پس از یک قانون عادی خواهد بود [Musy, 2001]:

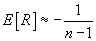
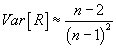
پس از اندرسون، والد و وولهاویتز آزمون غیر پارامتری ضریب همبستگی را ایجاد کردند که با استفاده از رابطه زیر محاسبه می شود:

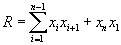
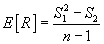
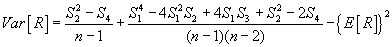
با:

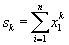
اختلافات همبستگی kρ_k یک سری زمانی ثابت با این تعریف می شود:

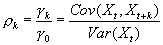
اتو کواریانس از طریق 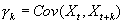 یک سری مشاهده x₁, x₂, ..., x_n تخمین زده می شود:

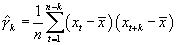
3. آزمون های متعاقب ماهیت اطلاعات. در هیدرولوژی بسته به شرایط خاص هیدرولوژیکی شرایط مختلفی وجود دارد. گاهی اوقات لازم است فقط یک نوع داده (بارندگی، دما و تبخیر) برای جریان محلی یا جریان منطقه ای کنترل شود و گاهی اوقات کنترل انواع مختلف داده ها (تخلیه بارندگی، سرعت دما- سرعت باد) برای محلی و جریان منطقه ای. (جزئیات بیشتر را می توان در Musy, "e-drology", 2001 یافت)

منابع

Musy, A. 1998. Hydrologie appliquée, Cours polycopié d'hydrologie générale, Lausanne, Suisse.

Musy, A. 2001. e-drologie. Ecole Polytechnique Fédérale, Lausanne, Suisse.

Shaw, E. M. 1984. Hydrology in practice, Second edition. T.J. Press Ltd., Cornwall, United Kingdom.

Vladimirescu, I. 1978. Hidrologie. Ed. Didactica si Pedagogica, Bucuresti, Romania.

مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

پروژه تخصصی در لینکدین

×

 براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح