zip_path = tf.keras.utils.get_file(
    origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
    fname='jena_climate_2009_2016.csv.zip',
    extract=True)
csv_path, _ = os.path.splitext(zip_path)

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip
13574144/13568290 [==============================] - 1s 0us/step

df = pd.read_csv(csv_path)
# slice [start:stop:step], starting from index 5 take every 6th record.
df = df[5::6]

date_time = pd.to_datetime(df.pop('Date Time'), format='%d.%m.%Y %H:%M:%S')

df.head()

plot_cols = ['T (degC)', 'p (mbar)', 'rho (g/m**3)']
plot_features = df[plot_cols]
plot_features.index = date_time
_ = plot_features.plot(subplots=True)

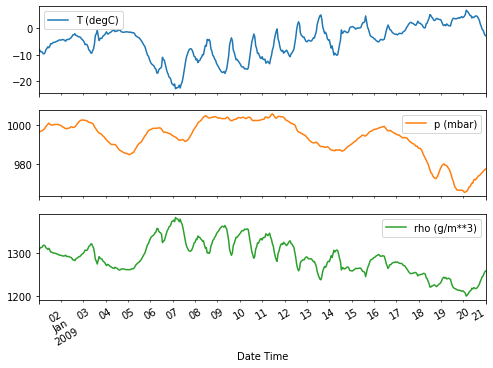
plot_features = df[plot_cols][:480]
plot_features.index = date_time[:480]
_ = plot_features.plot(subplots=True)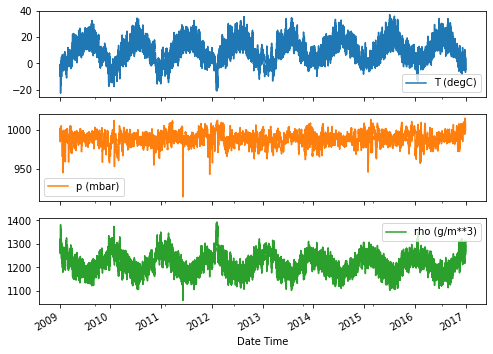

مهندسی ویژگی

قبل از عمیق شدن برای ساخت یک مدل، مهم است که اطلاعات خود را درک کنید، و مطمئن شوید که داده های قالب بندی شده مناسب را از مدل عبور می دهید.

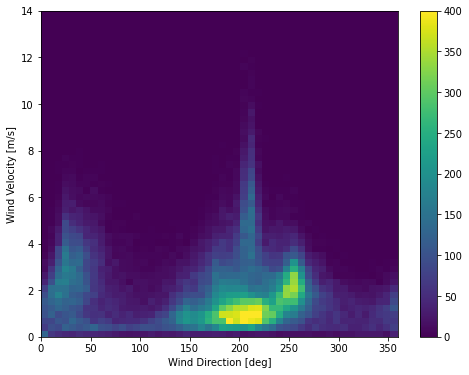
باد

آخرین ستون داده ها، wd بر حسب واحد deg، جهت باد را به واحد درجه نشان می دهد. زاویه ها ورودی مدل خوبی ایجاد نمی کنند، 360 درجه و 0 درجه باید نزدیک به یکدیگر باشند و به آرامی دور آن را بپیچانند. اگر وزش باد نباشد، جهت نباید مهم باشد.

در حال حاضر توزیع داده های باد به این شکل است:

plt.hist2d(df['wd (deg)'], df['wv (m/s)'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind Direction [deg]')
plt.ylabel('Wind Velocity [m/s]')

Text(0, 0.5, 'Wind Velocity [m/s]')

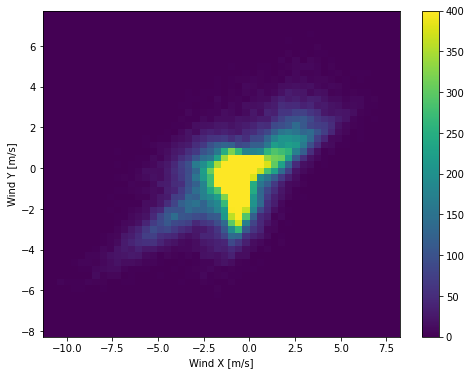
اگر ستون های جهت باد و سرعت را به بردار باد تبدیل کنید، تفسیر این برای مدل آسان تر خواهد بود:

wv = df.pop('wv (m/s)')
max_wv = df.pop('max. wv (m/s)')

# Convert to radians.
wd_rad = df.pop('wd (deg)')*np.pi / 180

# Calculate the wind x and y components.
df['Wx'] = wv*np.cos(wd_rad)
df['Wy'] = wv*np.sin(wd_rad)

# Calculate the max wind x and y components.
df['max Wx'] = max_wv*np.cos(wd_rad)
df['max Wy'] = max_wv*np.sin(wd_rad)

توزیع بردارهای باد برای تفسیر صحیح مدل بسیار ساده تر است.

plt.hist2d(df['Wx'], df['Wy'], bins=(50, 50), vmax=400)
plt.colorbar()
plt.xlabel('Wind X [m/s]')
plt.ylabel('Wind Y [m/s]')
ax = plt.gca()
ax.axis('tight')

(-11.305513973134667, 8.24469928549079, -8.27438540335515, 7.7338312955467785)

زمان

به همین ترتیب ستون Date Time بسیار مفید است، اما در این فرم رشته ای نیست. با تبدیل آن به ثانیه شروع کنید:

timestamp_s = date_time.map(datetime.datetime.timestamp)

مشابه جهت باد، زمان بر حسب ثانیه ورودی مفیدی نیست. به عنوان داده های آب و هوا، دارای تناوب روزانه و سالانه است. روش های زیادی وجود دارد که می توانید با تناوب مقابله کنید.

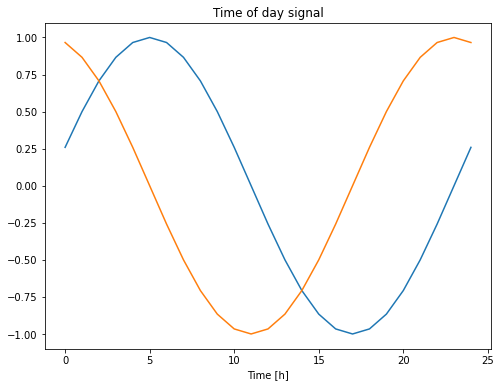
یک روش ساده برای تبدیل آن به یک سیگنال قابل استفاده، استفاده از sin و cos برای تبدیل زمان برای پاک کردن سیگنال های "Time of day" و "Time of year" است:

day = 24*60*60
year = (365.2425)*day

df['Day sin'] = np.sin(timestamp_s * (2 * np.pi / day))
df['Day cos'] = np.cos(timestamp_s * (2 * np.pi / day))
df['Year sin'] = np.sin(timestamp_s * (2 * np.pi / year))
df['Year cos'] = np.cos(timestamp_s * (2 * np.pi / year))

plt.plot(np.array(df['Day sin'])[:25])
plt.plot(np.array(df['Day cos'])[:25])
plt.xlabel('Time [h]')
plt.title('Time of day signal')

Text(0.5, 1.0, 'Time of day signal')

این به مدل امکان دسترسی به مهمترین ویژگیهای فرکانس را می دهد. در این حالت شما پیش از موعد می دانید کدام فرکانس ها مهم هستند.

اگر نمی دانید، می توانید فرکانس های مهم را با استفاده از fft.  تعیین کنید. برای بررسی فرضیات ما، در اینجا tf.signal.rfft دما در طول زمان است. به قله های واضح در فرکانس های نزدیک به 1/year  و 1/day توجه داشته باشید:

fft = tf.signal.rfft(df['T (degC)'])
f_per_dataset = np.arange(0, len(fft))

n_samples_h = len(df['T (degC)'])
hours_per_year = 24*365.2524
years_per_dataset = n_samples_h/(hours_per_year)

f_per_year = f_per_dataset/years_per_dataset
plt.step(f_per_year, np.abs(fft))
plt.xscale('log')
plt.ylim(0, 400000)
plt.xlim([0.1, max(plt.xlim())])
plt.xticks([1, 365.2524], labels=['1/Year', '1/day'])
_ = plt.xlabel('Frequency (log scale)')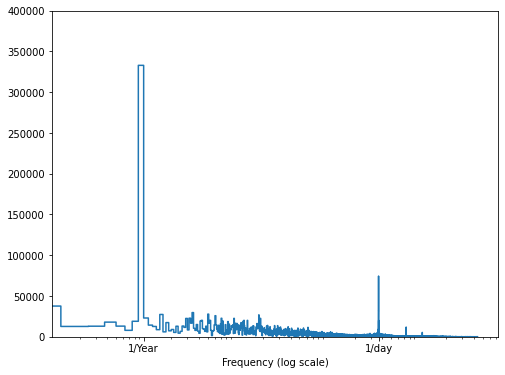

تقسیم داده ها

ما برای مجموعه ها، اعتبار سنجی و آزمون از تقسیم (70٪، 20٪، 10٪) استفاده خواهیم کرد. توجه داشته باشید که داده ها قبل از تقسیم به طور تصادفی تغییر نمی کنند. این به دو دلیل است.

این اطمینان را می دهد که خرد کردن داده ها در پنجره های نمونه های متوالی هنوز امکان پذیر است.

این اطمینان حاصل می کند که نتایج اعتبار سنجی / آزمون واقع بینانه تر هستند و پس از آموزش مدل، روی داده های جمع آوری شده ارزیابی می شوند.

column_indices = {name: i for i, name in enumerate(df.columns)}

n = len(df)
train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]

num_features = df.shape[1]

نرمال سازی داده ها

مقیاس گذاری ویژگی ها قبل از آموزش شبکه عصبی مهم است. عادی سازی یا نرمال سازی روش معمول انجام این مقیاس بندی است. میانگین را از آن کم کنید و سپس با انحراف معیار هر ویژگی تقسیم کنید.

میانگین و انحراف معیار فقط باید با استفاده از داده های آموزش محاسبه شود تا مدل ها به مقادیر مجموعه های اعتبار سنجی و آزمون دسترسی نداشته باشند.

همچنین جای بحث دارد که هنگام آموزش، مدل نباید به مقادیر آینده در مجموعه آموزش دسترسی داشته باشد و این عادی سازی باید با استفاده از میانگین متحرک انجام شود. این تمرکز بر آموزش نیست و مجموعه های تأیید و آزمایش اطمینان می دهند که (تا حدودی) معیارهای صحیحی دریافت می کنند. بنابراین به منظور سادگی در این آموزش از یک میانگین ساده استفاده می شود.

train_mean = train_df.mean()
train_std = train_df.std()

train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std

اکنون به توزیع ویژگی ها نگاه کنید. بعضی از ویژگی ها دارای دنباله طولانی هستند، اما هیچ خطای واضحی مانند مقدار سرعت باد 9999- وجود ندارد.

df_std = (df - train_mean) / train_std
df_std = df_std.melt(var_name='Column', value_name='Normalized')
plt.figure(figsize=(12, 6))
ax = sns.violinplot(x='Column', y='Normalized', data=df_std)
_ = ax.set_xticklabels(df.keys(), rotation=90)